练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f(x)=
    x-1
    x2+x+2
    (x＞1)    的值域是
     
    ．
    考点：函数的值域
    专题：计算题
    分析：先求出函数的导数，令导数值为零，找出单调区间，从而找到函数的最值，得出值域．
    解答： 解：f′（x）=
    x2+x+2-(x-1)(2x+1)
    (x2+x+2)2

    =
    -x2+2x+3
    (x2+x+2)2

    =
    -(x-3)(x+1)
    (x2+x+2)2
    （x＞1），
    令f′（x）=0，解得：x=3，x=-1（舍），
    ∴x=3把定义域分成（1，3]和（3，+∞）两部分，
    在区间（1，3]上，f′（x）＞0，f（x）是增函数，
    在区间（3，+∞）上，f′（x）＜0，f（x）是减函数，
    ∴f（x）max=f（3）=
    1
    7
    ，
    又∵x＞1，∴x-1＞0，而x2+x+2=(x+
    1
    2
    )    2    +
    7
    4
    ＞0，
    ∴f（x）＞0，
    ∴函数f（x）的值域为：（0，
    1
    7
    ]，
    故答案为：（0，
    1
    7
    ]．
    点评：本题是一道求函数的值域的问题，求函数值域时有多重方法，利用求导是其中的一个．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（α）=
    sin(π-α)•cos(2π-α)•tan(-π+α)
    sin(-π+α)•tan(-α+3π)
    ．
    （1）化简f（α）；
    （2）若f（α）=
    1
    8
    ，且
    π
    4
    ＜α＜
    π
    2
    ，求cosα-sinα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点P（x，y）的坐标满足条件
    x≤1
    y≤2
    2x+y-2≥0
    ，则
    y
    x
    的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义：min{a，b}=
    a，a≤b
    b，a＞b
    ，在区域
    0≤x≤2
    0≤y≤6
    内任取一点P（x，y），则x、y满足min{x2+x+2y，x+y+4}=x2+x+2y的概率为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=x3cosx+1，若f（a）=-2012，则f（-a）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    “x∈{3，a}”是不等式2x2-5x-3≥0成立的一个充分不必要条件，则实数a的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题：
    ①平面A′FG⊥平面ABC；
    ②BC∥平面A′DE；
    ③三棱锥A′-DEF的体积最大值为
    1
    64
    a3；
    ④动点A′在平面ABC上的射影在线段AF上；
    ⑤二面角A′-DE-F大小的范围是[0，
    π
    2
    ]．
    其中正确的命题是（　　）
    A、①③④B、①②③④
    C、①②③⑤D、①②③④⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x∈（0，
    π
    2
    ）且f（cosx）=sin
    x
    2
    ，则f（
    1
    2
    ）=（　　）
    A、
    2
    5
    B、
    1
    5
    C、
    1
    2
    D、
    7
    10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

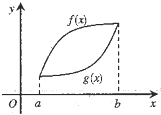    已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（　　）
    A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率
    B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率
    C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率
    D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率

    查看答案和解析>>

    同步练习册答案