
| A. | $[{1,\frac{3}{2}})$ | B. | $[{\frac{3}{2},+∞})$ | C. | [1,2) | D. | $[{\frac{3}{2},2})$ |
分析 先确定函数的定义域然后求导数fˊ(x),解关于导函数的不等式,求出f(x)的单调区间,根据子区间(k-1,k+1)是单调函数,建立不等关系,解之即可.
解答 解:∵f(x)定义域为(0,+∞),
∴f′(x)=4x-$\frac{1}{x}$=$\frac{(2x+1)(2x-1)}{x}$,
令f′(x)>0,解得:x>$\frac{1}{2}$
令f′(x)<0,解得:0<x<$\frac{1}{2}$,
∴f(x)在(0,$\frac{1}{2}$)递减,在($\frac{1}{2}$,+∞)递增,
∵f(x)在(k-1,k+1)内是单调函数,
∴k-1≥$\frac{1}{2}$,解得,k≥$\frac{3}{2}$,
故选:B.
点评 本题主要考查了对数函数的导数,以及利用导数研究函数的单调性等基础知识,考查计算能力,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.属于基础题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 生产产量y(万盒) | 4 | 4 | 5 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 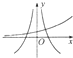 | B. | 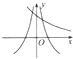 | C. | 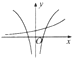 | D. | 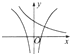 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2$\sqrt{2}$,$\frac{π}{4}$) | B. | (-2$\sqrt{2}$,$\frac{π}{4}$) | C. | (2$\sqrt{2}$,$\frac{3π}{4}$) | D. | (2$\sqrt{2}$,-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 997个 | B. | 954个 | C. | 682个 | D. | 3 个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com