
分析 利用对数的换底公式可得:a1•a2•a3•…•an=$\frac{lg3}{lg2}×\frac{lg4}{lg3}$×…×$\frac{lg(n+2)}{lg(n+1)}$=log2(n+2),要使log2(n+2)为整数,则n+2必须为2k(k∈N*)形式的数,即可得出.
解答 解:a1•a2•a3•…•an=$\frac{lg3}{lg2}×\frac{lg4}{lg3}$×…×$\frac{lg(n+2)}{lg(n+1)}$=log2(n+2),
要使log2(n+2)为整数,则n+2必须为2k(k∈N*)形式的数,
∴在区间(15,2015)内的所有劣数为30,62,126,254,510,1022,
其和=30+62+126+254+510+1022=2004,
故答案为:2004.
点评 本题考查了对数的换底公式、2k(k∈N*)形式的数,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若b?α,c∥α,则c∥b | B. | 若c∥α,c⊥β,则α⊥β | C. | 若c∥α,α⊥β,则c⊥β | D. | 若b?α,b∥c,则c∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-1,-$\frac{1}{3}$] | C. | (-∞,-1)∪[-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
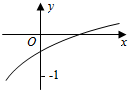 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com