
甲、乙两人进行围棋比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为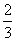 ,则甲以31的比分获胜的概率为( )
,则甲以31的比分获胜的概率为( )
A.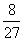 B.
B.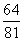
C.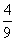 D.
D.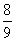
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
位于直角坐标原点的一个质点P按下列规则移动:质点每次移动一个单位,移动的方向为向左或向右,并且向左移动的概率为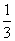 ,向右移动的概率为
,向右移动的概率为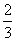 ,则质点P移动五次后位于点(1,0)的概率是( )
,则质点P移动五次后位于点(1,0)的概率是( )
A.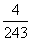 B.
B.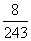
C.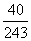 D.
D.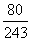
查看答案和解析>>
科目:高中数学 来源: 题型:
小波以游戏方式决定是参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6,A7,A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队.
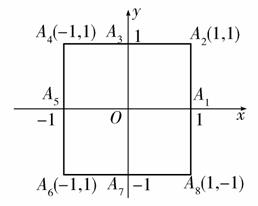
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次.在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知参赛选手甲在A区和B区每次投篮进球的概率分别为 或
或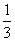 .
.
(1)如果选手甲以在A、B区投篮得分的期望较高者为选择投篮区的标准,问选手甲应该选择在哪个区投篮?
(2)求选手甲在A区投篮得分高于在B区投篮得分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com