
分析 设DG=x,则AG=2x,AB=3x,∠BAD=θ,由余弦定理求得cosθ的表达式,进而得出sinθ,求出三角形的面积关于x的函数,根据二次函数的性质求得面积的最大值.
解答 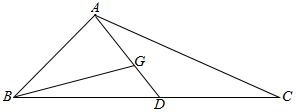 解:设DG=x,则AG=2x,∴AB=AD=3x,设∠BAD=θ,
解:设DG=x,则AG=2x,∴AB=AD=3x,设∠BAD=θ,
则在△ABG中,由余弦定理得cosθ=$\frac{A{B}^{2}+A{G}^{2}-B{G}^{2}}{2AB×AG}$=$\frac{13{x}^{2}-4}{12{x}^{2}}$.
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\sqrt{1-(\frac{13{x}^{2}-4}{12{x}^{2}})^{2}}$=$\frac{1}{12{x}^{2}}$$\sqrt{-25{x}^{4}+104{x}^{2}-16}$.
∴S△ABC=2S△ABD=2×$\frac{1}{2}×AB×AD×sinθ$=$\frac{3}{4}$$\sqrt{-25{x}^{4}+104{x}^{2}-16}$.
令f(x)=-25x4+104x2-16=-25(x2-$\frac{52}{25}$)2+$\frac{5{2}^{2}}{25}-16$.
∴当x2=$\frac{52}{25}$时,f(x)取得最大值$\frac{5{2}^{2}}{25}-16$=92.16.
∴S△ABC的最大值为$\frac{3}{4}×\sqrt{92.16}$=7.2.
故答案为7.2.
点评 本题考查了函数最值的应用,根据条件设出变量,根据三角形的面积公式以及三角函数的关系是解决本题的关键,利用二次函数的性质即可求出函数的最值,考查学生的运算能力.运算量较大,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
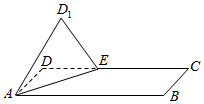 在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com