
分析 化简f(x)=ax2+|x-1|,从而讨论去绝对值号,再讨论确定函数的单调性及单调区间,从而求最小值.
解答 解:当a∈(0,4),b=1时,
f(x)=ax2+|x-1|,
当x∈(1,2]时,f(x)=ax2+x-1,
故f(x)在(1,2]上是增函数;
当x∈[0,1]时,f(x)=ax2-x+1
=a(x-$\frac{1}{2a}$)2+1-$\frac{1}{4a}$;
当0<$\frac{1}{2a}$<1,即a>$\frac{1}{2}$时,
f(x)在(0,$\frac{1}{2a}$)上单调递减,在[$\frac{1}{2a}$,1]单调递增;
结合函数的连续性知,
fmin(x)=f($\frac{1}{2a}$)=1-$\frac{1}{4a}$;
当$\frac{1}{2a}$≥1,即0<a≤$\frac{1}{2}$时,
f(x)在(0,1)上单调递减;
结合函数的连续性知,
fmin(x)=f(1)=a.
点评 本题考查了绝对值函数的应用及分类讨论的思想方法应用,属于中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | tan2θ | B. | cot4θ | C. | tan4θ | D. | cot2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2187 | C. | 2188 | D. | -2187 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
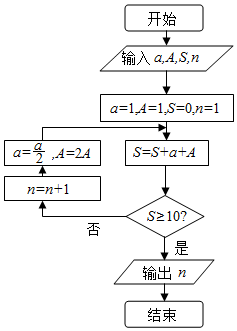 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )| A. | 4 | B. | 5 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 1440 | C. | 720 | D. | 2160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com