
分析 (1)问题转化为$b≥\frac{1}{2}{x^2}+x-{e^x}$恒成立,令g(x)=$\frac{1}{2}$x2+x-ex,根据函数的单调性求出b的范围即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出g(a)的表达式,根据函数的单调性求出g(a)的最小值即可.
解答 解:(1)当a=e时,f(x)=x-ex,
原题分离参数得$b≥\frac{1}{2}{x^2}+x-{e^x}$恒成立,
令g(x)=$\frac{1}{2}$x2+x-ex,g′(x)=x+1-ex,g″(x)=1-ex<0,
故g′(x)在[0,+∞)递减,g′(x)<g′(0)=0,
故g(x)在[0,+∞)递减,
g(x)≤g(0)=-1,
故b≥-1;
(2)f'(x)=1-axlna,
①当0<a<1时,ax>0,lna<0,
所以f'(x)>0,所以f(x)在R上为单增函数,无极大值;
②当a>1时,设方程f'(x)=0的根为t,
则有${a^t}=\frac{1}{lna}$,即$t={log_a}\frac{1}{lna}=\frac{{ln\frac{1}{lna}}}{lna}$,
所以f(x)在(-∞,t)上为增函数,在(t,+∞)上为减函数,
所以f(x)的极大值为$f(t)=t-{a^t}=\frac{{ln\frac{1}{lna}}}{lna}-\frac{1}{lna}$,
即$g(a)=\frac{{ln\frac{1}{lna}}}{lna}-\frac{1}{lna}$,因为a>1,所以$\frac{1}{lna}>0$,
令$x=\frac{1}{lna}$则$\frac{{ln\frac{1}{lna}}}{lna}-\frac{1}{lna}=xlnx-x$,
设h(x)=xlnx-x,x>0,则$h'(x)=lnx+x•\frac{1}{x}-1=lnx$,
令h'(x)=0,得x=1,
所以h(x)在(0,1)上为减函数,在(1,+∞)上为增函数,
所以h(x)得最小值为h(1)=-1,
即g(a)的最小值为-1,
此时a=e.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查函数恒成立问题,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\frac{{\sqrt{3}}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
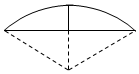 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).
为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com