
分析 (Ⅰ)由题意求出F1,F2的坐标,利用坐标表示写出$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$,根据点P在椭圆C上,求出$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最小值;
(Ⅱ)设出l的方程以及点A、B的坐标,直线方程与椭圆方程联立,消去y利用判别式△>0和根与系数的关系,
由弦长公式和点到直线的距离求出三角形的面积,再求面积的最大值.
解答 解:(Ⅰ)∵F1,F2分别为椭圆C:$\frac{x^2}{8}+\frac{y^2}{2}=1$的左、右焦点,
∴${F_1}(-\sqrt{6},0)$,${F_2}(\sqrt{6},0)$,
∴$\overrightarrow{P{F_1}}=(-\sqrt{6}-{x_0},-{y_0})$,$\overrightarrow{P{F_2}}=(\sqrt{6}-{x_0},{y_0})$,
∴$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}={x_0}^2+{y_0}^2-6$;
又点P(x0,y0)在椭圆C上,∴$\frac{{{x_0}^2}}{8}+\frac{{{y_0}^2}}{2}=1$,即${y_0}^2=2-\frac{{{x_0}^2}}{4}$,
∴$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}={x_0}^2+2-\frac{{{x_0}^2}}{4}-6=-4+\frac{{3{x_0}^2}}{4}$($-2\sqrt{2}≤{x_0}≤2\sqrt{2}$),
∴当x0=0时,$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最小值为-4;
(Ⅱ)设l的方程为$y=\frac{1}{2}x+b$,点A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}y=\frac{1}{2}x+b\\ \frac{x^2}{8}+\frac{y^2}{2}=1\end{array}\right.$,消去y得x2+2bx+2b2-4=0,
令△=4b2-8b2+16>0,解得-2<m<2;
由根与系数的关系得x1+x2=-2b,${x_1}{x_2}=2{b^2}-4$,
由弦长公式得$|AB|=\sqrt{1+\frac{1}{4}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{5(4-{b^2})}$,
又点P到直线l的距离为$d=\frac{|b|}{{\sqrt{1+\frac{1}{4}}}}=\frac{2|b|}{{\sqrt{5}}}$,
∴${S_{△PAB}}=\frac{1}{2}|AB|d=\frac{1}{2}×\frac{2|b|}{{\sqrt{5}}}×\sqrt{5(4-{b^2})}$=$\sqrt{{b^2}(4-{b^2})}$$≤\frac{{{b^2}+4-{b^2}}}{2}=2$,
当且仅当$b=±\sqrt{2}$时,等号成立,
∴△PAB面积最大值为2.
点评 本题考查了直线与圆锥曲线的综合应用问题,也考查了弦长公式与点到直线距离的应用问题,是综合性题.


科目:高中数学 来源: 题型:选择题
| A. | 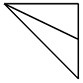 | B. | 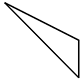 | C. | 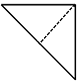 | D. | 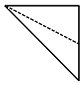 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 1-2a | C. | 0 | D. | 21-2a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 12 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1] | C. | [-1,1] | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com