
分析 (1)要使a∈A,即(a+a)(a2+a2+1)=0有解,解方程即可;
(2)集合A有且仅有两个元素,得到集合中方程(x+a)(x2+ax+1)=0有两个不等实根,分析其解的情况,得到a 的取值.
解答 解:(1)已知集合A={x∈R|(x+a)(x2+ax+1)=0}.要使a∈A,即(a+a)(a2+a2+1)=0有解,解得a=0;所以存在实数a=0,使得a∈A;
(2)若集合A有且仅有两个元素,说明方程(x+a)(x2+ax+1)=0有两个不等实根,所以①x+a=0且x2+ax+1=0有两个不等于-a的相等实根;解得a=2或-2;
②x2+ax+1=0有两个不相等的实根,其中的一个根为-a;此情况不合题意;
故实数a的取值集合{2,-2}.
点评 本题考查了元素与集合关系;关键是由题意,正确分析集合中方程解的情况.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6$\sqrt{3}$ | B. | -6$\sqrt{3}$ | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,AB是平面α外的固定斜线段,B为斜足,若点C在平面α内运动,且∠CAB等于直线AB与平面α所成的角,则动点C的轨迹为( )
如图,AB是平面α外的固定斜线段,B为斜足,若点C在平面α内运动,且∠CAB等于直线AB与平面α所成的角,则动点C的轨迹为( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
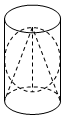 利用浮力原理巧妙地称出了皇冠中黄金的重量的阿基米德,在他的墓碑上有一幅几何图案,如图所示,因为阿基米德很欣赏这三者的体积之比为V圆锥:V球:V圆柱=1:2:3,他还得出球的表面积与它的外切圆柱的表面积之比等于它们的体积之比,都等于2:3.
利用浮力原理巧妙地称出了皇冠中黄金的重量的阿基米德,在他的墓碑上有一幅几何图案,如图所示,因为阿基米德很欣赏这三者的体积之比为V圆锥:V球:V圆柱=1:2:3,他还得出球的表面积与它的外切圆柱的表面积之比等于它们的体积之比,都等于2:3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com