
分析 (Ⅰ)由条件得an=2Sn-1+1(n≥2),与条件式相减可得$\frac{{a}_{n+1}}{{a}_{n}}$=3,再验证$\frac{{a}_{2}}{{a}_{1}}=3$即可得{an}为等比数列,从而求出通项公式;
(Ⅱ)化简得bn=(3n-1)•3n-1,使用错位相减法求和即可.
解答 解:(Ⅰ)∵an+1=2Sn+1,∴an=2Sn-1+1,(n≥2),
两式相减得:an+1-an=2an,即$\frac{{a}_{n+1}}{{a}_{n}}$=3.
又n=1时,a2=2a1+1=3,∴$\frac{{a}_{2}}{{a}_{1}}=3$,
∴{an}是以1为首项,以3为公比的等比数列.
∴an=3n-1.
(Ⅱ)bn=(3n-1)an=(3n-1)•3n-1,
∴Tn=2•30+5•31+8•32+…+(3n-1)•3n-1,①
∴3Tn=2•31+5•32+8•33+…+(3n-1)•3n,②
∴-2Tn=2+32+33+34+…+3n-(3n-1)•3n
=$\frac{3(1-{3}^{n})}{1-3}$-1-(3n-1)•3n=($\frac{5}{2}-3n$)•3n-$\frac{5}{2}$,
∴Tn=($\frac{3n}{2}$-$\frac{5}{4}$)•3n+$\frac{5}{4}$.
点评 本题考查了等比数列的通项公式,错位相减法数列求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4π}$ | B. | $\frac{π-2}{π}$ | C. | $\frac{3π-2}{4π}$ | D. | $\frac{2}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
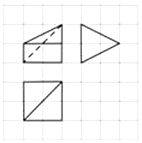
| A. | $10+\sqrt{5}$ | B. | $7+3\sqrt{5}$ | C. | $8+\sqrt{5}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
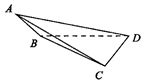 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com