Question

6．如图，平面PCBM⊥平面ABC，∠PCB=90°，PM∥BC，直线AM与直线PC所成的角为45°，又AC=1，BC=2PM=2，∠ACB=90°．
（1）求证：AC⊥BM；
（Ⅱ）求二面角M-AB-C的余弦值．

Answer 1

分析 （1）由平面 PCMB⊥平面ABC，AC⊥BC，AC⊥平面PCMB，BM?平面 PMBC，则AC⊥BM；
（2）取BC中点N，连结 AN、MN，平面PCMB⊥平面ABC，则PC⊥BC，PC⊥平面ABC，MN⊥平面 ABC，作NH⊥AB于H，连结MH，则由三垂线定理知，AB⊥MH，从而∠MHN为二面角M-AB-C的平面角，分别求得MN和NH，则tan∠MHN=$\frac{MN}{NH}$=$\frac{\frac{\sqrt{6}}{3}}{\frac{\sqrt{5}}{5}}$=$\frac{\sqrt{30}}{3}$，故二面角 M-AB-C 的大小为arctan$\frac{\sqrt{30}}{3}$；方法二：如图，以 C 为原点建立空间直角坐标系 C-xyz，设P（0，0，z₀ ）（z₀ ＞0），求得$\overrightarrow{AM}$，$\overrightarrow{AB}$，则平面MAB的一个法向量为$\overrightarrow{n}$，则cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{丨\overrightarrow{m}丨•丨\overrightarrow{n}丨}$，即可求得二面角M-AB-C的余弦值．

解答 解：（1）∵平面PCMB⊥平面ABC，AC⊥BC，AC?平面 ABC，
∴AC⊥平面PCMB
又∵BM?平面PMBC
∴AC⊥BM；

方法一：（2）取BC中点N，则CN=1，连结AN、MN，
∵平面PCMB⊥平面ABC，平面PCBM∩平面ABC=BC，PC⊥BC
∴PC⊥平面ABC
∵PM∥CN，PM=CN，
∴MN∥PC，
∴MN⊥平面ABC
作NH⊥AB于H，连结MH，则由三垂线定理知，AB⊥MH
从而∠MHN为二面角M-AB-C的平面角，
∵直线AM与直线PC所成的角为60°
∴∠AMN=60°
在△ACN 中，由勾股定理得AN=$\sqrt{2}$，
在Rt△AMN 中，MN=AN•cot∠AMN=$\sqrt{2}$•$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{6}}{3}$，
在Rt△BNH 中，NH=sin∠ABC=BN•$\frac{AC}{AB}$=1×$\frac{\sqrt{5}}{5}$=$\frac{\sqrt{5}}{5}$，
在Rt△MNH 中，tan∠MHN=$\frac{MN}{NH}$=$\frac{\frac{\sqrt{6}}{3}}{\frac{\sqrt{5}}{5}}$=$\frac{\sqrt{30}}{3}$，
故二面角M-AB-C的大小为arctan$\frac{\sqrt{30}}{3}$ _；
（2）方法二：如图，以C为原点建立空间直角坐标系 C-xyz，
设P（0，0，z₀ ）（z₀ ＞0），有B（0，2，0），A（1，0，0），M（0，1，z₀ ）
_{$\overrightarrow{AM}$} =（-1，1，z₀ ），_{$\overrightarrow{CP}$} =（0，0，z₀ ）
由直线AM与直线PC所成的角为60°，得 $\overrightarrow{AM}$•$\overrightarrow{CP}$=丨$\overrightarrow{AM}$丨•丨$\overrightarrow{CP}$ 丨cos60°，

即${z}_{0}^{2}$=$\frac{1}{2}$$\sqrt{{z}_{0}^{2}+2}$•z₀，解得：z₀=$\frac{\sqrt{6}}{3}$，

∴_{$\overrightarrow{AM}$} =（-1，1，$\frac{\sqrt{6}}{3}$），$\overrightarrow{AB}$=（-1，2，0），
设平面 MAB 的一个法向量为$\overrightarrow{n}$=（x₁，y₁，z₁），
则$\left\{\begin{array}{l}{-{x}_{1}+{y}_{1}+\frac{\sqrt{6}}{3}{z}_{1}=0}\\{-{x}_{1}+2{y}_{1}=0}\end{array}\right.$，取z₁=$\sqrt{6}$，解得：$\overrightarrow{n}$=（4，2，$\sqrt{6}$），
取平面ABC的一个法向量为$\overrightarrow{m}$=（0，0，1），
则cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{丨\overrightarrow{m}丨•丨\overrightarrow{n}丨}$=$\frac{\sqrt{6}}{1×\sqrt{16+4+6}}$=$\frac{\sqrt{39}}{13}$，
故二面角 M-AB-C 的大小为 arctan$\frac{\sqrt{30}}{3}$．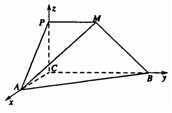

点评 本题主要考查异面直线所成的角、平面与平面垂直、二面角等有关知识，考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、属于中档题．