
| A. | a<-2 | B. | a>-2 | C. | a>-$\frac{1}{2}$ | D. | a<-$\frac{1}{2}$ |
分析 f′(x)=aeax+2=0,当a≥0无解,无极值.当a<0时,x=$\frac{1}{a}$ln(-$\frac{2}{a}$),由于函数y=eax+2x,x∈R有大于零的极值点,可得a的取值范围.
解答 解:f′(x)=aeax+3,令f′(x)=0即aeax+2=0,
当a≥0无解,∴无极值.
当a<0时,x=$\frac{1}{a}$ln(-$\frac{2}{a}$),
当x>$\frac{1}{a}$ln(-$\frac{2}{a}$),f′(x)>0;x<$\frac{1}{a}$ln(-$\frac{2}{a}$)时,f′(x)<0.
∴$\frac{1}{a}$ln(-$\frac{2}{a}$)为极大值点,
∴$\frac{1}{a}$ln(-$\frac{2}{a}$)>0,解之得a<-2,
故选:A.
点评 本题考查了利用导数研究函数的极值,考查了推理能力与计算能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
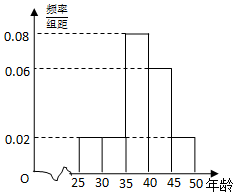 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2<k<10 | B. | k>10 | C. | k<2或k>10 | D. | 以上答案均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com