
分析 由题意和正余弦定理可得a,c的值,由同角三角函数的基本关系可得sinB,代入三角形的面积公式计算可得.
解答 解:在△ABC中由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,
由sinC=2sinA,则c=2a,
cosB=$\frac{1}{4}$,sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{15}}{4}$,
由余弦定理可知:b2=a2+c2-2accosB,即32=a2+(2a)2-2a•2a×$\frac{1}{4}$,
解得a=$\frac{3}{2}$,c=3,
△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×$\frac{3}{2}$×3×$\frac{\sqrt{15}}{4}$=$\frac{9\sqrt{15}}{16}$,
故答案为:$\frac{9\sqrt{15}}{16}$,.
点评 本题考查三角形的面积,涉及正余弦定理的应用,属基础题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
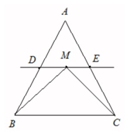 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
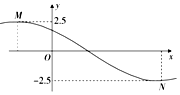 已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com