
| A. | 这样的三角形不存在 | |
| B. | 这样的三角形存在,且为锐角三角形 | |
| C. | 这样的三角形存在,且为直角三角形 | |
| D. | 这样的三角形存在,且为钝角三角形 |
分析 设高2,3,4对应三边分别为a,b,c,根据面积相等求出三边之比,利用余弦定理求出cosA的值小于0,即可做出判断.
解答 解:设高2,3,4对应三边分别为a,b,c,
根据面积相等得:$\frac{1}{2}$a•2=$\frac{1}{2}$b•3=$\frac{1}{2}$c•4,
整理得:2a=3b=4c,即a:b:c=6:4:3,
由余弦定理得:cosA=$\frac{{3}^{2}+{4}^{2}-{6}^{2}}{2×3×4}$=-$\frac{11}{24}$<0,
∴A为钝角,即△ABC为钝角三角形,
则这样的三角形存在,且为钝角三角形,
故选:D.
点评 此题考查了余弦定理,以及余弦函数的性质,熟练掌握余弦定理是解本题的关键.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
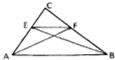 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )| A. | 3 | B. | -3 | C. | 0 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{π}{2}$,0] | C. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 锻练时间 | 男生 | 女生 | 合计 |
| 少于1小时 | 5 | 15 | 20 |
| 不少于1小时 | 20 | 10 | 30 |
| 合 计 | 25 | 25 | 50 |
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com