
分析 (1)求导数,分别令导数大于零、小于零解得函数的增减区间,注意结合定义域对字母a进行讨论;
(2)求出函数g(x)在定义域内的最大值,令其小于或等于1,解出a即可.
解答 解:(1)由已知$f′(x)=\frac{1}{x}-a=\frac{1-ax}{x}$(x>0).
当a=0时,$f′(x)=\frac{1}{x}>0$,故函数f(x)在定义域内是增函数.
当a≠0时,令f′(x)=0得x=$\frac{1}{a}$.
若a<0,由f′(x)>0得x$>\frac{1}{a}$,结合定义域得f′(x)>0在定义域内恒成立,故函数f(x)在定义域内是增函数;
若a>0,由f′(x)>0得$0<x<\frac{1}{a}$,f′(x)<0得x$>\frac{1}{a}$.故函数f(x)的增区间为(0,$\frac{1}{a}$),减区间为[$\frac{1}{a},+∞$).
综上,当a≤0时,f(x)在(0,+∞)内是增函数;当a>0时,f(x)的增区间为(0,$\frac{1}{a}$),减区间为[$\frac{1}{a},+∞$).
(2)①当0<x≤1时,g(x)=f(x),由(1)知:
当a≤0时,f(x)在(0,1]内递增,所以f(x)max=f(1)=ln1-a≤1,即-1≤a≤0即为所求;
当$0<\frac{1}{a}<1$,即a>1时,f(x)在(0,$\frac{1}{a}$]上递增,在$(\frac{1}{a},1]$上递减,故此时f(x)max=f($\frac{1}{a}$)=$ln\frac{1}{a}-1≤1$,解得$a≥\frac{1}{{e}^{2}}$,故此时a>1为所求;
当$\frac{1}{a}≥1$,即0<a≤1时,f′(x)>0在(0,1)上恒成立,故此时f(x)为增函数,所以f(x)max=f(1)=ln1-a≤1,解得a≥-1,故0<a≤1符合题意.
所以当0<x≤1时,所求a的范围是a≥-1.
②当-1≤x≤0时,
若a<0,则g(x)=ax-1为减函数,此时g(x)max=g(-1)=-a-1≤1,解得-2≤a<0,
若a=0,g(x)=-1<1显然成立,
若a>0,g(x)=ax-1是增函数,所以g(x)max=g(0)=-1≤1显然成立.
所以当-1≤x≤0时,所求a的范围是a≥-2.
综合①②可知,若函数g(x)≤1恒成立,只需a≥-1即可.
点评 本题考查了利用导数研究函数单调性的方法,以及与分段函数有关的不等式恒成立问题,注意此类问题仍然遵循分段处理的原则.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | 这样的三角形不存在 | |
| B. | 这样的三角形存在,且为锐角三角形 | |
| C. | 这样的三角形存在,且为直角三角形 | |
| D. | 这样的三角形存在,且为钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
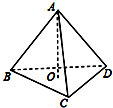 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )| A. | 三条中线的交点 | B. | 三角平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三垂直平分线的交点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))的离心率为$\frac{1}{2}$,点F1、F2分别是椭圆的左、右焦点,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))的离心率为$\frac{1}{2}$,点F1、F2分别是椭圆的左、右焦点,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD.若∠BPC=90°,PB=$\sqrt{2}$,PC=2则四棱锥P-ABCD的体积最大值为$\frac{2\sqrt{6}}{9}$.
如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD.若∠BPC=90°,PB=$\sqrt{2}$,PC=2则四棱锥P-ABCD的体积最大值为$\frac{2\sqrt{6}}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | (0,1) | C. | (0,1] | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com