
分析 (1)利用三角函数的诱导公式即可求出$sin({\frac{π}{4}+θ})$的值;
(2)由$cos({\frac{π}{4}-θ})=\frac{{\sqrt{2}}}{10}$可得$sinθ+cosθ=\frac{1}{5}$,两边平方得$2sinθcosθ=-\frac{24}{25}$,再结合θ的范围即可求出sinθ-cosθ的值,则sin4θ-cos4θ的值可求.
解答 解:(1)∵$cos(\frac{π}{4}-θ)=sin(θ+\frac{π}{4})$,
∴$sin({\frac{π}{4}+θ})$=$\frac{\sqrt{2}}{10}$;
(2)由$cos({\frac{π}{4}-θ})=\frac{{\sqrt{2}}}{10}$可得$sinθ+cosθ=\frac{1}{5}$,
两边平方得$2sinθcosθ=-\frac{24}{25}$,
∵θ∈(0,π),sinθ>0,∴cosθ<0,sinθ-cosθ>0,
∵${({sinθ-cosθ})^2}=1-2sinθcosθ=\frac{49}{25}$,∴$sinθ-cosθ=\frac{7}{5}$.
sin4θ-cos4θ=sin2θ-cos2θ=$\frac{7}{25}$.
点评 本题考查了三角函数的诱导公式,考查了同角三角函数基本关系式的应用,是中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:填空题
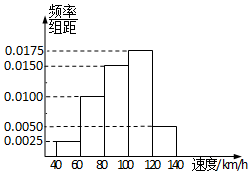 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
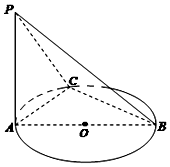 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{4}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com