
| 连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
| 甲 | 70 | 5 | 60 |
| 乙 | 60 | 5 | 25 |
分析 (Ⅰ)直接由题意结合图表列关于x,y所满足得不等式组,化简后即可画出二元一次不等式所表示的平面区域;
(Ⅱ)写出总收视人次z=60x+25y.化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 (Ⅰ)解:由已知,x,y满足的数学关系式为$\left\{\begin{array}{l}70x+60y≤600\\ 5x+5y≥30\\ x≤2y\\ x≥0\\ y≥0\end{array}\right.$,即$\left\{\begin{array}{l}7x+6y≤60\\ x+y≥6\\ x-2y≤0\\ x≥0\\ y≥0\end{array}\right.$.
该二元一次不等式组所表示的平面区域如图: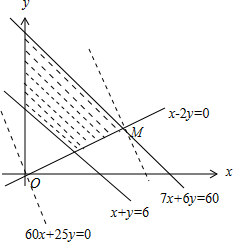
(Ⅱ)解:设总收视人次为z万,则目标函数为z=60x+25y.
考虑z=60x+25y,将它变形为$y=-\frac{12}{5}x+\frac{z}{25}$,这是斜率为$-\frac{12}{5}$,随z变化的一族平行直线.
$\frac{z}{25}$为直线在y轴上的截距,当$\frac{z}{25}$取得最大值时,z的值最大.
又∵x,y满足约束条件,
∴由图可知,当直线z=60x+25y经过可行域上的点M时,截距$\frac{z}{25}$最大,即z最大.
解方程组$\left\{\begin{array}{l}7x+6y=60\\ x-2y=0\end{array}\right.$,得点M的坐标为(6,3).
∴电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多.
点评 本题考查解得线性规划的应用,考查数学建模思想方法及数形结合的解题思想方法,是中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{2}{3}$π | B. | x=-$\frac{1}{12}$π | C. | x=$\frac{1}{3}$π | D. | x=$\frac{5}{12}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2,4} | C. | {1,2,4,5} | D. | {x∈R|-1≤x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [2,4] | C. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | D. | [$\sqrt{5}$-1,$\sqrt{5}$+1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$+1 | D. | $\sqrt{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
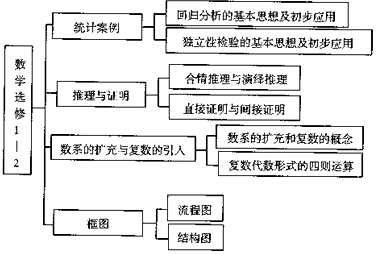
| A. | 推理与证明 | B. | 统计案例 | ||
| C. | 数系的扩充与复数的引入 | D. | 框图 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
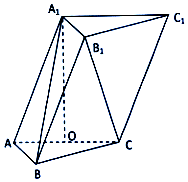 如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com