Question

15．函数f（x）=2x³-6x+k，x∈R．
（1）当k=5时，求函数f（x）在点（2，f（2））处的切线方程．
（2）若函数f（x）=2x³-6x+k在R上只有一个零点，求常数k的取值范围．

Answer 1

分析 （1）先求出函数的导函数，再求出函数在（2，-6）处的导数即斜率，易求切线方程．
（2）求出函数的导数，求出极值点，判断单调性，通过极值的符号，结合函数的零点，求解即可．

解答 解（1）∵f（x）=2x³-6x+5，f′（x）=6x²-6，
∴f（x）在点点（2，f（2））即（2，9）处的切线的斜率为k=f′（2）=18．
∴切线的方程为y-9=18（x-2）即y=18x-27
（2）f（x）=2x³-6x+k，则f′（x）=6x²-6，令f′（x）=0，得x=-1或x=1，
可知f（x）在（-1，1）上是减函数，f（x）在（-∞，-1）和（1，+∞）上为增函数．
f（x）的极大值为f（-1）=4+k，f（x）的极小值为f（1）=-4+k．
要使函数f（x）只有一个零点，只需4+k＜0或-4+k＞0（如图所示）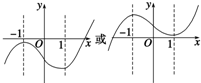

即k＜-4或k＞4．∴k的取值范围是（-∞，-4）∪（4，+∞）．

点评 本题考查导数的几何意义，函数的极值以及函数的零点的判断，考查学生的计算能力，解题的关键是利用导数的几何意义求出切线的斜率，属于中档题．