
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | 2 | C. | 4 | D. | 2+$\sqrt{3}$ |
分析 由a+c=2b,且$sinB=\frac{4}{5}$,可得B为锐角,cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3}{5}$.由题意可得:$\frac{3}{2}$=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac×$\frac{4}{5}$,化为:ac=$\frac{15}{4}$,又b2=a2+c2-2ac×$\frac{3}{5}$,a+c=2b,联立解得b.
解答 解:由a+c=2b,且$sinB=\frac{4}{5}$,可得B为锐角,cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3}{5}$.
由题意可得:$\frac{3}{2}$=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac×$\frac{4}{5}$,化为:ac=$\frac{15}{4}$,
又b2=a2+c2-2ac×$\frac{3}{5}$,a+c=2b,
联立解得b=2,
故选:B.
点评 本题考查了三角形面积计算公式、余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
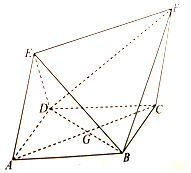 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)为R上增函数 | B. | 函数f(x)为R上减函数 | ||
| C. | 函数f(x)在R上单调性不确定 | D. | 命题q为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8};\frac{π}{4}$ | B. | $\frac{1}{4};\frac{π}{2}$ | C. | $\frac{1}{2};π$ | D. | 1;2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4,5} | B. | {3,4,5} | C. | {3,4,5,6} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com