
分析 设A(0,b),B(x,0),C(a,b-y),由x-a)2+(y-b)2=x2+b2=a2+y2
得△ABC为等边△,设△ABC边长为m,∠OAB=θ,(0$≤θ≤\frac{π}{6}$)
过C作CH⊥x轴与H,则∠ACH=θ-$\frac{π}{6}$,a=mcos($θ-\frac{π}{6}$),b=mcosθ即可求解.
解答 解:如图设A(0,b),B(x,0),C(a,b-y)
∵(x-a)2+(y-b)2=x2+b2=a2+y2
∴△ABC为等边△,设△ABC边长为m,∠OAB=θ,(0$≤θ≤\frac{π}{6}$)
过C作CH⊥x轴与H,则∠ACH=θ-$\frac{π}{6}$,∴$a=mcos(θ-\frac{π}{6})$
b=mcosθ
∴$\frac{b}{a}=\frac{cosθ}{cos(θ-\frac{π}{6})}=\frac{1}{\frac{\sqrt{3}}{2}+\frac{1}{2}tanθ}$
∴当θ=0时,$(\frac{b}{a})_{nax}=\frac{2\sqrt{3}}{3}$
故答案为:$\frac{2\sqrt{3}}{3}$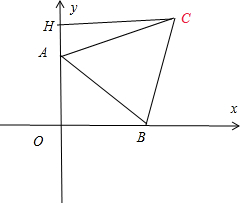
点评 本题考查了通过解析法处理最值问题,考查了转化思想、运算能力,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{2}(\sqrt{2}-1)π$ | B. | $\frac{25}{4}(3-2\sqrt{2})π$ | C. | $25(3-2\sqrt{2})π$ | D. | $\frac{125}{6}(5\sqrt{2}-7)π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com