练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．直线l过点（1，0）且与曲线y=-$\frac{1}{{e}^{x}}$相切，设其倾斜角为α，则α=（　　）
    A．30°B．60°C．45°D．135°

    分析 设出切点坐标，求出函数的导数，利用导数的几何意义求出切线的斜率，由点斜式求出切线方程，代入点（1，0），解方程即可得到结论．

    解答 解：∵y=-$\frac{1}{{e}^{x}}$，
    ∴函数的导数为y′=$\frac{1}{{e}^{x}}$，
    设切点坐标为（x0，-$\frac{1}{{e}^{{x}_{0}}}$），
    ∴切线方程为y+$\frac{1}{{e}^{{x}_{0}}}$=$\frac{1}{{e}^{{x}_{0}}}$（x-x0），
    ∵切线l过点（1，0），
    ∴$\frac{1}{{e}^{{x}_{0}}}$=$\frac{1}{{e}^{{x}_{0}}}$（1-x0），
    解得x0=0，
    ∴$\frac{1}{{e}^{{x}_{0}}}$=1=tanα，
    ∴α=45°，
    故选C．

    点评 本题主要考查导数的几何意义，考查直线方程的形式，求函数的导数是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，已知直线l的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数），以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=$\frac{p}{1-cosθ}$（p＞0）
    （1）写出直线l的极坐标方程和曲线C的直角坐标方程；
    （2）若直线l与曲线C相交于A，B两点，求$\frac{1}{|OA|}$+$\frac{1}{|OB|}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

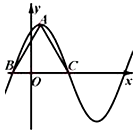    9．函数f（x）=6cos2$\frac{ωx}{2}$+2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为正三角形．
    （1）求函数f（x）的值域及ω的值；
    （2）将函数y=f（x）的图象上各点的横坐标缩短到原来的$\frac{π}{8}$，纵坐标不变，得到函数y=g（x）的图象，求函数y=g（x）在区间[-$\frac{π}{2}$，0]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如表数据：
    单价x（元）88.28.48.68.89
    销量y（件）908483m7568
    根据最小二乘法建立的回归直线方程为$\widehaty=-20x+250$，
    （1）试求表格中m的值；
    （2）预计在今后的销售中，销量与单价仍然服从建立的回归方程，且该产品的成本是5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在△ABC中，角A，B，C所对的边分别为a，b，c，已知cosC+（cosA-$\sqrt{3}$sinA）cosB=0
    （1）求角B的大小；
    （2）若b=$\frac{1}{2}$，求△ABC的周长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．复数f（x）=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}，x∈[-1.1]}\\{\frac{1}{x}，x∈（1，+∞）}\end{array}\right.$，则$\int_0^2{f（x）}$dx=$\frac{π}{4}$+ln2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知非零向量$\overrightarrow{AB}，\overrightarrow{AC}$满足$（\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|cosB}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|cosC}}）•\overrightarrow{BC}=\overrightarrow{AB}•\overrightarrow{AC}$，则△ABC为（　　）
    A．等腰三角形B．锐角三角形C．钝角三角形D．直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知锐角三角形ABC的内角A，B，C的对边分别为a，b，c，且$a=bcosC+\frac{{\sqrt{3}}}{3}csinB$．，
    （1）求B；
    （2）若b=2，求ac的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知函数f（x）=x2+2x+a．若g（x）=$\frac{1}{{e}^{x}}$，对任意x1∈[$\frac{1}{2}$，2]，存在x2∈[$\frac{1}{2}$，2]，使f（x1）≤g（x2）成立，则实数a的取值范围是（　　）
    A．（-∞，$\frac{\sqrt{e}}{e}$-8]B．[$\frac{\sqrt{e}}{e}$-8，+∞）C．[$\sqrt{2}$，e）D．（-$\frac{\sqrt{3}}{3}$，$\frac{e}{2}$]

    查看答案和解析>>

    同步练习册答案