
分析 由题意作图辅助,从而利用平面向量的线性运算化简即可.
解答 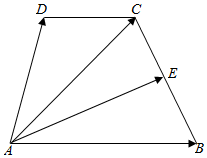 解:由题意作图如右图,
解:由题意作图如右图,
∵AB∥CD,AB=2CD,∴$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{AB}$,
∵E为BC中点,
∴$\overrightarrow{AE}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$)=$\frac{1}{2}$($\overrightarrow{AD}$+$\overrightarrow{DC}$+$\overrightarrow{AB}$)
=$\frac{1}{2}$($\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AB}$)=$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{3}{4}$$\overrightarrow{AB}$,
又∵$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,
∴x=$\frac{1}{2}$,y=$\frac{3}{4}$,
故x+y=$\frac{5}{4}$
故答案为:$\frac{5}{4}$.
点评 本题考查了平面向量的线性运算的几何表示与数形结合的思想应用.


科目:高中数学 来源: 题型:解答题
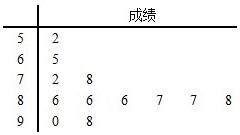 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{7}$,+∞) | B. | [$\frac{1}{7}$,$\frac{1}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{7}$]∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )
在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com