
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
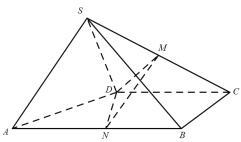
(1)求证:平面![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值,不存在说出理由.
的值,不存在说出理由.
【答案】(1)证明见解析;(2)存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,此时
,此时![]()
【解析】
(1)通过平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,进而可证明平面
,进而可证明平面![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 面
面![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,可证明
,可证明![]() 为二面角
为二面角![]() 的平面角的补角,通过计算可得
的平面角的补角,通过计算可得![]() ,假设存在点
,假设存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可得
,可得![]() 为二面角
为二面角![]() 的平面角,计算可得
的平面角,计算可得![]() ,进而可得
,进而可得![]() .
.
(1)证明:![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ;
;
(2)如图:![]() 平面
平面![]() 平面
平面![]() ,则过点
,则过点![]() 作
作![]() 面
面![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
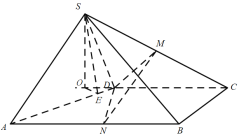
![]() ,
,
![]() 面
面![]() ,则
,则![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角的补角,
的平面角的补角,
则![]() ,
,
又![]() ,
,
两式相乘得![]() ,
,
即![]() ,
,![]() ,
,
![]() ,
,
假设存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]()
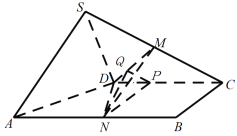
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
可得![]() 面
面![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
设![]() ,因为
,因为![]() ,四边形
,四边形![]() 为矩形,则
为矩形,则![]() ,
,
![]() ,则
,则![]() ,
,
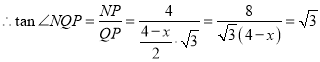 ,
,
解得![]() ,
,
此时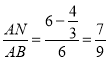 .
.
存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,此时
,此时![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拉丁舞,又称拉丁风情舞或自由社交舞,它是拉丁人民在漫长的历史长河中形成的,包含伦巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜爱.某艺术培训机构为了调查本校学院对拉丁舞的学习情况,分别在刚学习了一个季度的本校大班(8岁以下)及种子班(8岁以上)的学员中各随机抽取了15名学员进行摸底考试,这30名学员考试成绩的茎叶图如图所示.

规定:成绩不低于85分,则认为成绩优秀;成绩低于85分,则认为成绩一般.
(1)根据上述数据填写下列2×2联表:
成绩优秀 | 成绩一般 | 总计 | |
大班 | |||
种子班 | |||
总计 |
判断是否有95%的把握认为成绩优秀或成绩一般与学员的年龄有关;
(2)在大班及种子班的参加摸底考试且成绩优秀的学员中以分层抽样的方式抽取6名学员进行特别集训,集训后,再对这6名学员进行测试,按测试成绩,取前3名授予“舞蹈小精灵”称号,在被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率.
参考公式及数据: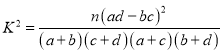 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
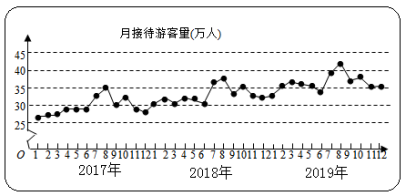
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2)![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() 为
为![]() 上异于
上异于![]() 的一点,当
的一点,当![]() 面积最大时,求点
面积最大时,求点![]() 到
到![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() .
.
(1)当![]() 时,判断曲线
时,判断曲线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当曲线![]() 上有且只有一点到曲线
上有且只有一点到曲线![]() 的距离等于
的距离等于![]() 时,求曲线
时,求曲线![]() 上到曲线
上到曲线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() .现沿对角线
.现沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() .点
.点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() 、
、![]() 、
、![]() 、
、![]() 四点共面.
四点共面.

(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: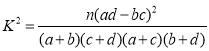 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com