
 某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.分析 (1)由题意及茎叶图得“高个子”共8名队员,“非高个子”共12名队员,共抽取5名队员,故从“高个子”队员中抽取2名队员,记为A,B,从“非高个子”中抽取3名队员,记为a,b,c,利用列举法能求出从这5名队员中随机选出2名队员,这2名队员中有“高个子”的概率.
(2)由茎叶图知“高个子”男队员有4名,记为D,E,F,G,“高个子”女队员有4名,记为d,e,f,g,利用列举法能求出这5名队员中,恰好男女“高个子”各1名队员的概率.
解答 解:(1)由题意及茎叶图得:
“高个子”共8名队员,“非高个子”共12名队员,
共抽取5名队员,故从“高个子”队员中抽取2名队员,记为A,B,
从“非高个子”中抽取3名队员,记为a,b,c,
从中选出2名队员共有${C}_{5}^{2}$=10种选法,分别为:
AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,
这2名队员中有“高个子”的选法有7种,分别是:
AB,Aa,Ab,Ac,Ba,Bb,Bc,
故选取2名队员中有“高个子”的概率是p1=$\frac{7}{10}$.
(2)由茎叶图知“高个子”男队员有4名,记为D,E,F,G,
“高个子”女队员有4名,记为d,e,f,g,
从中抽取2名队员,共有${C}_{8}^{2}$=28种抽法,分别为:
DE,DF,DG,Dd,De,Df,Dg,EF,EG,Ed,Ee,Ef,Eg,FG,
Fd,Fe,Ff,Fg,gd,Ge,Gf,Gg,de,df,dg,ef,eg,fg,
其中,男女“高个子”各1名队员的抽法有16种,
∴这5名队员中,恰好男女“高个子”各1名队员的概率p2=$\frac{16}{28}=\frac{4}{7}$.
点评 本题考查概率的求法,考查列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方体ABCD-A1B1C1D1中,点P在正方体表面运动,如果${S_{△AB{D_1}}}={S_△}_{PB{D_1}}$,那么这样的点P共有( )
如图,在正方体ABCD-A1B1C1D1中,点P在正方体表面运动,如果${S_{△AB{D_1}}}={S_△}_{PB{D_1}}$,那么这样的点P共有( )| A. | 2个 | B. | 4个 | C. | 6个 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
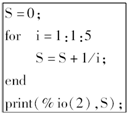
| A. | $\frac{137}{60}$ | B. | $\frac{133}{60}$ | C. | $\frac{131}{60}$ | D. | $\frac{121}{60}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$-$\frac{3}{10}$i | B. | $\frac{1}{10}$+$\frac{3}{10}$i | C. | $\frac{9}{10}$+$\frac{3}{10}$i | D. | $\frac{1}{10}$-$\frac{3}{10}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com