练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．以下程序运行的结果是（　　）
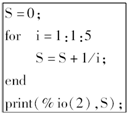
    A．$\frac{137}{60}$B．$\frac{133}{60}$C．$\frac{131}{60}$D．$\frac{121}{60}$

    分析 该程序运行的结果是计算并输出S=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$的值．

    解答 解：根据题意，该程序运行的结果是计算并输出
    S=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=$\frac{137}{60}$．
    故选：A．

    点评 本题考查了程序语言的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．如果（x+$\frac{a}{x}$）（x-$\frac{2}{x}$）4的展开式中各项系数之和为2，则展开式中x的系数是（　　）
    A．8B．-8C．16D．-16

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，正方体ABCD-A1B1C1D1中，M，N分别为AB，BC的中点．
    （1）求证：平面B1MN⊥平面BB1D1D；
    （2）当点P在DD1上运动时，是否都有MN∥平面A1C1P，证明你的结论；
    （3）若P是D1D的中点，试判断PB与平面B1MN是否垂直？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某校男女篮球队各有10名队员，现将这20名队员的身高绘制成茎叶图（单位：cm）．男队员身高在180cm以上定义为“高个子”，女队员身高在170cm以上定义为“高个子”，其他队员定义为“非高个子”．按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员．
    （1）从这5名队员中随机选出2名队员，求这2名队员中有“高个子”的概率；
    （2）求这5名队员中，恰好男女“高个子”各1名队员的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，-π≤φ≤π）一个周期的图象（如图），则这个函数的一个解析式为（　　）
    A．y=2sin（3x-$\frac{π}{2}$）B．y=2sin（3x-$\frac{π}{6}$）C．y=2sin（3x+$\frac{π}{6}$）D．y=2sin（$\frac{3}{2}$x+$\frac{π}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求下列函数的导数：
    （1）y=2x5-3x2-4
    （2）y=3cos x-4sin x
    （3）y=（2x+3）2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的2×2列联表：
      做不到“光盘” 能做到“光盘”
     男 45 10
     女 30 15
    表：
    P（K2≥k）0.100.050.025
    k2.7063.8415.024
    经计算K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$参照附表，得到的正确结论是（　　）
    A．在犯错误的概率不超过5%的前提下，认为“该市居民能否做到‘光盘’与性别有关”
    B．在犯错误的概率不超过2.5%的前提下，认为“该市居民能否做到‘光盘’与性别有关”
    C．有90%以上的把握认为“该市居民能否做到‘光盘’与性別无关”
    D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$下，函数z=3x-y的最小值是（　　）
    A．9B．1C．-3D．-9

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．函数f（x）=1+logax（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-2=0上，则m+n=2．

    查看答案和解析>>

    同步练习册答案