
 已知函数y=Asin(ωx+φ)(A>0,ω>0,-π≤φ≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,-π≤φ≤π)一个周期的图象(如图),则这个函数的一个解析式为( )| A. | y=2sin(3x-$\frac{π}{2}$) | B. | y=2sin(3x-$\frac{π}{6}$) | C. | y=2sin(3x+$\frac{π}{6}$) | D. | y=2sin($\frac{3}{2}$x+$\frac{π}{2}$) |
分析 根据函数图象求出A,ω和φ的值进行求解即可.
解答 解:由图象知A=2,$\frac{T}{4}$=$\frac{π}{2}$-$\frac{π}{3}$=$\frac{π}{6}$,
即函数的周期T=$\frac{2π}{3}$,
∵T=$\frac{2π}{ω}$=$\frac{2π}{3}$,
∴ω=3,
则y=2sin(3x+φ),
由五点对应法得$\frac{π}{3}$×3+φ=$\frac{π}{2}$,
则φ=$\frac{π}{2}$-π=-$\frac{π}{2}$,
则函数的解析式为y=2sin(3x-$\frac{π}{2}$),
故选:A
点评 本题主要考查函数解析式的求解,结合图象求出ω 和φ的值是解决本题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点,且P点坐标为($\frac{1}{2}$,1),|$\overrightarrow{OQ}$|=2.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点,且P点坐标为($\frac{1}{2}$,1),|$\overrightarrow{OQ}$|=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
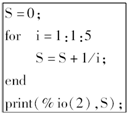
| A. | $\frac{137}{60}$ | B. | $\frac{133}{60}$ | C. | $\frac{131}{60}$ | D. | $\frac{121}{60}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=$\frac{sin2x}{{x}^{2}}$ | B. | f(x)=$\frac{cos2x}{{x}^{2}}$ | C. | f(x)=$\frac{co{s}^{2}x}{2x}$ | D. | f(x)=$\frac{cos2x}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若c,d 与a,b都相交,则c,d是异面直线 | |
| B. | 若c∥a,d∥b,则 c,d 是异面直线 | |
| C. | 若c,d 与 a,b 都异面,则 c,d 是异面直线 | |
| D. | 若c,d 与 a,b 都垂直,则 c∥d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不了解 | 了解 | 总计 | |
| 女性 | 25 | b | 50 |
| 男性 | c | 35 | 50 |
| 总计 | x | y | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com