
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
分析 作出图形,取AB中点D,并连接OD,从而有OD⊥AB,而$\overrightarrow{OA}=\overrightarrow{OD}+\overrightarrow{DA}$,可设△ABC的内角A,B,C所对的边分别为a,b,c,然后在$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=m•\overrightarrow{OA}$的两边同时乘以$\overrightarrow{AB}$,进行数量积的运算便可得到$\frac{cosB}{sinC}•{c}^{2}+\frac{cosC}{sinB}•bccosA=-\frac{m}{2}•{c}^{2}$,由正弦定理即可得到$cosB+cosCcosA=-\frac{m}{2}•sinC$,从而解出$m=\frac{-2(cosB+cosCcosA)}{sinC}$,而cosB=-cos(A+C),这样便可求出m=-2sinA,从而便得出m的值.
解答 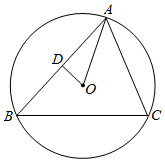 解:如图,取AB中点D,则$\overrightarrow{OA}=\overrightarrow{OD}+\overrightarrow{DA}$,OD⊥AB;
解:如图,取AB中点D,则$\overrightarrow{OA}=\overrightarrow{OD}+\overrightarrow{DA}$,OD⊥AB;
∴$\overrightarrow{OD}•\overrightarrow{AB}=0$;
设△ABC的三个内角A,B,C所对的边分别为a,b,c;
由$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=m•\overrightarrow{OA}$得,$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=m(\overrightarrow{OD}+\overrightarrow{DA})$;
两边同乘以$\overrightarrow{AB}$得:$\frac{cosB}{sinC}•{\overrightarrow{AB}}^{2}+\frac{cosC}{sinB}•\overrightarrow{AC}•\overrightarrow{AB}$=$m(\overrightarrow{OD}+\overrightarrow{DA})•\overrightarrow{AB}$;
即$\frac{cosB}{sinC}•{c}^{2}+\frac{cosC}{sinB}•bccosA=-\frac{m}{2}•{c}^{2}$;
∴$\frac{cosB}{sinC}•c+\frac{cosC}{sinB}•bcosA=-\frac{m}{2}•c$;
由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2r$,∴b=2rsinB,c=2rsinC,代入上式整理得:
$cosB+cosCcosA=-\frac{m}{2}•sinC$;
∴$m=\frac{-2(cosB+cosCcosA)}{sinC}$=$\frac{-2[-cos(A+C)+cosCcosA]}{sinC}$=-2sinA;
又∠A=60°;
∴$m=-2sin60°=-\sqrt{3}$.
故选:A.
点评 考查向量加法的几何意义,向量垂直的充要条件,以及数量积的计算公式,正弦定理,两角和的余弦公式.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
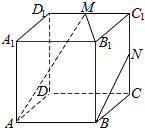
| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=0.4x+0.9 | B. | $\widehat{y}$=2x-5.5 | C. | $\widehat{y}$=-2x+10.5 | D. | $\widehat{y}$=-0.3x+4.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | -7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com