练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    甲、乙、丙、丁、戊五人并排站成一排，如果甲必须站在乙的右边（甲、乙可以不相邻）那么不同的排法共有（　　）
    A、24种B、60种
    C、90种D、120种
    考点：排列、组合的实际应用
    专题：排列组合
    分析：根据题意，首先计算五人并排站成一排的情况数目，进而分析可得，B站在A的左边与B站在A的右边是等可能的，使用倍分法，计算可得答案．
    解答： 解：根据题意，使用倍分法，
    五人并排站成一排，有A55种情况，
    而其中B站在A的左边与B站在A的右边是等可能的，则其情况数目是相等的，
    则B站在A的右边的情况数目为
    1
    2
    ×A55=60．
    故选B．
    点评：本题考查排列、组合的应用，注意使用倍分法时，注意必须保证其各种情况是等可能的．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若曲线x2+y2=9上各点的横坐标保持不变，纵坐标缩短为原来的一半，则所得曲线方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知i为虚数单位，则复数2i（1+i）的模是（　　）
    A、4
    B、2
    		2
    C、3
    		2
    D、8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在底面半径为3，高为4+2
    		3
    的圆柱形有盖容器内，放入一个半径为3的大球后，再放入与球面、圆柱侧面及上底面均相切的小球，则放入小球的个数最多为（　　）
    A、4B、5C、6D、7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    u
    =(-2，2，5)    ，
    v
    =(6，-4，4)    ，
    u
    ，
    v
    分别是平面α，β的法向量，则平面α，β的位置关系式（　　）
    A、平行
    B、垂直
    C、所成的二面角为锐角
    D、所成的二面角为钝角

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）的导函数为f′（x），且对任意x＞0，都有f′（x）＞
    f(x)
    x
    ．
    （Ⅰ）判断函数F（x）=
    f(x)
    x
    在（0，+∞）上的单调性；
    （Ⅱ）设x1，x2∈（0，+∞），证明：f（x1）+f（x2）＜f（x1+x2）；
    （Ⅲ）请将（Ⅱ）中的结论推广到一般形式，并证明你所推广的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    记者在街上随机抽取10人，在一个月内接到的垃圾短信条数统计的茎叶图如图：
    （Ⅰ）计算样本的平均数及方差；
    （Ⅱ）现从10人中随机抽出2名，设选出者每月接到的垃圾短信在10条以下的人数为X，求随机变量X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    2013年12月21日上午10时，省会首次启动重污染天气Ⅱ级应急响应，正式实施机动车车尾号限行，当天某报社为了解公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：
    年龄（岁） [15，25） [25，35） [35，45） [45，55） [55，65） [65，75]
    频数 5 10 15 10 5 5
    赞成人数 4 6 9 6 3 4
    （Ⅰ）完成被调查人员的频率分布直方图；
    （Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行进行追踪调查，记选中的4人中不赞成“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．

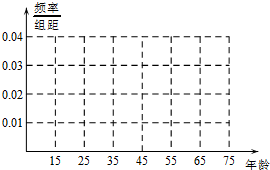
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点，
    （Ⅰ）求直线BC与A1C所成的角的度数． 
    （Ⅱ）求证：A1C∥平面BDE．

    查看答案和解析>>

    同步练习册答案