考点:导数在最大值、最小值问题中的应用,导数的加法与减法法则
专题:综合题,导数的综合应用
分析:(1)先求函数f(x)的导数,f′(x),再对k进行奇偶数讨论:1°当k 为奇数时;2°当k 为偶数时;分别得出导数值为正或负时的x的取值集合,最后综合即可;
(2)当k为奇数时,f′(x)=2(x+
),要证(1+b
n)
>e,即证(1+
)
n+1>e,两边取对数,即证ln(1+
)>
,设1+
=t,构造函数g(t)=lnt+
-1,利用导数工具研究其单调性即可证得lnt>1-
,最后利用累乘法即可证出S
2012-1<ln2012.
解答:
(1)解:函数f(x)的定义域为(0,+∞),又f′(x)=2x-2(-1)
k ,
1°当k 为奇数时,f′(x)=2x+
,∵x∈(0,+∞),∴f′(x)>0恒成立;
2°当k 为偶数时,f′(x)=
,∵x+1>0,∴f′(x)>0得x>1,即f(x)的单调增区间为(1,+∞),
综上所述,当k 为奇数时,f(x)的单调增区间为(0,+∞),当k 为偶数时,即f(x)的单调增区间为(1,+∞),
(2)当k为奇数时,f′(x)=2(x+
),
∴b
n=
f′(n)-n=
,S
n=1+
+
+…+
要证(1+b
n)
>e,即证(1+
)
n+1>e,两边取对数,
即证ln(1+
)>
设1+
=t,则n=
,
lnt>1-
(t>1),构造函数g(t)=lnt+
-1,
∵x>1,∴g′(t)=
-
>0
∴g(t)在(1,+∞)上是增函数,g(t)>g(1)>0
即lnt>1-
,∴(1+b
n)
>e,
S
2012-1=(1+
+
+…+
)-1=
+
+…+
,
∵ln(1+
)>
,
+
+…+
<ln2+ln(1+
)+…+ln(1+
)=ln2+ln
+…+ln
=ln(2×
×…×
)=ln2012,
∴
+
+…+
<ln2012,
点评:本小题主要考查利用导数研究函数的单调性、证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.



 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案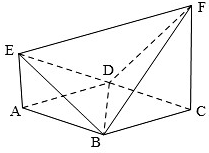 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC⊥平面ABCD,设EA=1,FC=2;