
 如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$.
如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$.分析 (1)由题意可得c=$\sqrt{5}$,再由弦长$\frac{2{b}^{2}}{a}$,运用直角三角形的面积公式,解方程可得a=3,b=2,进而得到椭圆方程;
(2)设过点M(-$\sqrt{5}$,0)的直线l:x=my-$\sqrt{5}$,代入椭圆方程,运用韦达定理,再由|PM|=2|MQ|,可得$\overrightarrow{PM}$=2$\overrightarrow{MQ}$,运用向量共线的坐标表示,解方程可得直线方程.
解答 解:(1)由题意可得c=$\sqrt{5}$,
将x=c代入椭圆方程可得y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=±$\frac{{b}^{2}}{a}$,
即有△OP0Q0的面积为$\frac{1}{2}$|PQ|•c=$\frac{4\sqrt{5}}{3}$,
即$\frac{{b}^{2}}{a}$=$\frac{4}{3}$,且a2-b2=5,
解得a=3,b=2,
即有椭圆方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1;
(2)设过点M(-$\sqrt{5}$,0)的直线l:x=my-$\sqrt{5}$,代入椭圆方程,
可得(4m2+9)y2-8$\sqrt{5}$my-16=0,
设P(x1,y1),Q(x2,y2),
y1+y2=$\frac{8\sqrt{5}m}{9+4{m}^{2}}$,y1y2=-$\frac{16}{9+4{m}^{2}}$,
由|PM|=2|MQ|,可得$\overrightarrow{PM}$=2$\overrightarrow{MQ}$,
即有-y1=2y2,代入韦达定理可得,
m2=$\frac{1}{4}$,可得m=±$\frac{1}{2}$,
故所求直线方程为2x+y+2$\sqrt{5}$=0或2x-y+2$\sqrt{5}$=0.
点评 本题考查椭圆的方程的求法,注意运用过焦点的弦长公式,考查直线方程和椭圆方程联立,运用韦达定理,以及向量共线的坐标表示,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
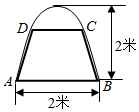 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
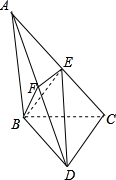 如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.
如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
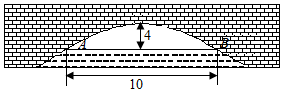 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com