
分析 利用辅助角公式化积.
(1)直接利用周期公式求得周期,再由相位的终边落在x轴上求得函数图象的对称中心;
(2)由x得范围求得f(x)的范围,把-2<f(x)-m<2在x∈[$\frac{π}{4},\frac{π}{2}$]上恒成立转化为f(x)-2<m<f(x)+2在x∈[$\frac{π}{4},\frac{π}{2}$]上恒成立得答案.
解答 解:f(x)=sin2x-$\sqrt{3}$cos2x=$2sin(2x-\frac{π}{3})$.
(1)函数的周期为T=$\frac{2π}{2}=π$.
由2x$-\frac{π}{3}=kπ$,得x=$\frac{kπ}{2}+\frac{π}{6},k∈Z$,
∴函数的对称中心为($\frac{kπ}{2}+\frac{π}{6},0$),k∈Z;
(2)由-2<f(x)-m<2在x∈[$\frac{π}{4},\frac{π}{2}$]上恒成立,
得f(x)-2<m<f(x)+2在x∈[$\frac{π}{4},\frac{π}{2}$]上恒成立,
∵x∈[$\frac{π}{4},\frac{π}{2}$],∴2x$-\frac{π}{3}$∈[$\frac{π}{6},\frac{2π}{3}$],则f(x)∈[1,2],
∴0<m<3.
∴实数m的取值范围是(0,3).
点评 本题考查三角函数中的恒等变换应用,考查了恒成立问题的求解方法,是中档题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 50 | C. | 100 | D. | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| ≥170cm | <170cm | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | -8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,+∞) | B. | [1,+∞) | C. | (0,+∞) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
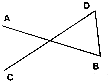
| A. | $\overrightarrow{AB}$-$\overrightarrow{CD}$ | B. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{CD}$ | C. | $\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{CD}$) | D. | -($\overrightarrow{AB}$-$\overrightarrow{CD}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com