
分析 由函数f(x)的解析式求得f(1)的值;由f(a)≤3,可得 $\left\{\begin{array}{l}{a<0}\\{{a}^{2}+2a≤3}\end{array}\right.$①,或 $\left\{\begin{array}{l}{a≥0}\\{{-a}^{2}≤3}\end{array}\right.$②,分别求得①、②的解集,再取并集,即得实数a的取值范围.
解答 解:由函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x<0}\\{-{x}^{2},x≥0}\end{array}\right.$,可得f(1)=-1.
由f(a)≤3,可得 $\left\{\begin{array}{l}{a<0}\\{{a}^{2}+2a≤3}\end{array}\right.$①,或 $\left\{\begin{array}{l}{a≥0}\\{{-a}^{2}≤3}\end{array}\right.$②.
解①求得-3≤a<0,解②求得a≥0,故f(a)≤3的解集为[-3,+∞),
故答案为:-1;[-3,+∞).
点评 本题主要考查分段函数的应用,一元二次不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
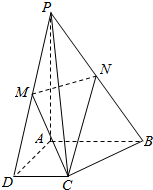 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com