
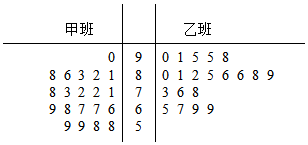
分析 根据题意,进入决赛的选手共有6名,拥有“优先挑战权”的选手共有3名;
对选手编号,用列举法求出基本事件数,计算所求的概率值.
解答 解:进入决赛的选手共有6名,其中拥有“优先挑战权”的选手共有3名;
设拥有“优先挑战权”的选手编号为1,2,3,其余3人编号为A,B,C.
被选中3人的编号所有可能的情况共20种,列举如下:
123,12A,12B,12C,13A,13B,13C,1AB,1AC,1BC,
23A,23B,23C,2AB,2AC,2BC,
3AB,3AC,3BC,
ABC;
其中拥有“优先挑战权”的选手恰有1名的情况共9种,如下:
1AB,1AC,1BC,2AB,2AC,2BC,3AB,3AC,3BC;
故所求的概率为$P=\frac{9}{20}$.
点评 本题考查了用列举法求古典概型的概率问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 16,$\sqrt{3}$ | B. | 18,$\sqrt{3}$ | C. | 16,$3\sqrt{3}$ | D. | 18,$3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
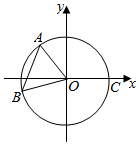 如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.
如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{3}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com