
分析 (1)(2)利用向量共线定理即可得出.
解答 解:(1)∵$\overrightarrow{a}$+λ$\overrightarrow{b}$=(1-3λ,2+2λ),∵($\overrightarrow{a}$+λ$\overrightarrow{b}$)∥$\overrightarrow{c}$,∴4(1-3λ)-3(2+2λ)=0,解得$λ=-\frac{1}{9}$.
(2)∵k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$和$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$共线,∴存在实数m,使得k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$=m($\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$),非零向量$\overrightarrow{{e}_{1}}$和$\overrightarrow{{e}_{2}}$不共线,
∴k=m,1=mk,
解得k=1或k=-1.
点评 本题考查了向量共线定理、共面向量基本定理,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
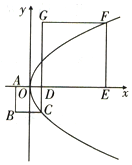 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com