设
（1）求
的表达式，并判断的奇偶性；
（2）试证明：函数的图象上任意两点的连线的斜率大于0；
（3）对于，当
时，恒有
求m的取值范围。
名题训练系列答案
期末集结号系列答案科目：高中数学 来源： 题型：解答题
已知函数
（1）若函数y=f(x)的图象切x轴于点（2，0），求a、b的值；
（2）设函数y="f(x)" 
的图象上任意一点的切线斜率为k，试求
的充要条件；（3）若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1，求证
。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
一片森林原来面积为
，计划每年砍伐一些树，且每年砍伐面积的百分比相等，当砍伐到面积的一半时，所用时间是10年，为保护生态环境，森林面积至少要保留原面积的
，已知到今年为止，森林剩余面积为原来的
.
（Ⅰ）求每年砍伐面积的百分比；
（Ⅱ）到今年为止，该森林已砍伐了多少年？
（Ⅲ）今后最多还能砍伐多少年？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本小题满分12分)
设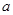
∈R，函数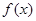
=
（
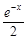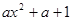），其中e是自然对数的底数．
（1）判断f (x)在R上的单调性；
（2）当– 1 <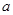< 0时，求f (x)在[1，2]上的最小值．
选做题：请考生从给出的3道题中任选一题做答，并在答题卡上把所选题目的题号用2B铅笔涂黑．注意所做题目的题号必须与所涂的题号一致，在答题卡选答区域指定位置答题．如果多做，则按所做的第一题计分．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
对于函数
，若存在x0∈R，使方程
成立，则称x0为的不动点，已知函数
（a≠0）．
（1）当
时，求函数的不动点；
（2）若对任意实数b，函数恒有两个相异的不动点，求a的取值范围；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
奇函数
时，
时，
综上，
，
代入
中，得
在
处取得极小值2．
的解析式；
，若对于任意
，总存在
，使得
，求实数
的取值范围．
（
且
）．
的定义域；
的
取值范围．
有三个不同的实根．
为奇函数，且在
上为增函数， 
， 若
对所有
都成立，求
的取值范围。