Question

8．在四面体ABCD中，下列条件不能得出AB⊥CD的是（　　）

• A． AB⊥BC且AB⊥BD
• B． AD⊥BC且AC⊥BD
• C． AC=AD且BC=BD
• D． AC⊥BC且AD⊥BD

Answer 1

分析 在几何体中选取边长的中点，运用等腰三角形的性质，直线平面的垂直，平面与平面的垂直问题判断即可得出答案．

解答 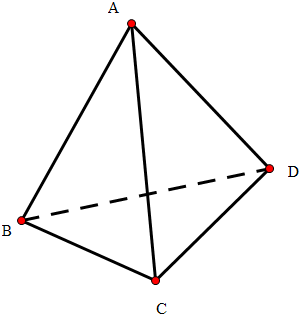解：①∵AB⊥BD，AB⊥BC，BD∩BC=B，
∴AB⊥面BCD，
∵CD?面BCD，
∴AB⊥CD，
②设A在面BCD射影为O，AO⊥面BCD，
∵AD⊥BC，AC⊥BD，
∴O为△BCD的垂心
连接BO，则BO⊥CD，AO⊥CD
∴CD⊥面ABO．
∵AB?面ABO．
∴AB⊥CD，
③取CD中点G，连接BG，AG，
∵AC=AD且BC=BD，
∴CD⊥BG，CD⊥AG，
∵BG∩AG=G，
∴CD⊥面ABG，
∵AB?面ABG
∴AB⊥CD，
综上选项A，B，C能够得出AB⊥CD，
故选：D

点评 本题综合考查了空间几何体中点直线，平面的垂直问题，关键是利用平面几何知识，空间直线平面的性质定理，判定定理转化直线的位置关系判断即可．