Question

7．已知|$\overrightarrow{OA}$|=3，|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，若$\overrightarrow{OP}$=$\frac{\sqrt{3}}{3}$$\overrightarrow{OA}$+$\overrightarrow{OB}$，则∠AOP=（　　）

• A． $\frac{π}{6}$
• B． $\frac{π}{3}$
• C． $\frac{2π}{3}$
• D． $\frac{5π}{6}$

Answer 1

分析 由题意建立平面直角坐标系，得到$\overrightarrow{OA}、\overrightarrow{OB}$的坐标，由$\overrightarrow{OP}$=$\frac{\sqrt{3}}{3}$$\overrightarrow{OA}$+$\overrightarrow{OB}$求得$\overrightarrow{OP}$的坐标，再由数量积求夹角公式得答案．

解答 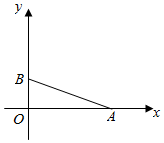解：由题意建立如图所示直角坐标系，
则$\overrightarrow{OA}$=（3，0），$\overrightarrow{OB}$=（0，1），
∴$\overrightarrow{OP}$=$\frac{\sqrt{3}}{3}$$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\frac{\sqrt{3}}{3}$（3，0）+（0，1）=（$\sqrt{3}，1$）．
∴cos∠AOP=$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}||\overrightarrow{OP}|}=\frac{3\sqrt{3}}{3×2}=\frac{\sqrt{3}}{2}$，
则∠AOP=$\frac{π}{6}$．
故选：A．

点评 本题考查平面向量的数量积运算，考查由数量积求向量的夹角，是中档题．