
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
分析 (1)由题意求出$\overline{x}$,$\overline{y}$,即可求解售额y的方差;
(2)根据$\overline{x}$,$\overline{y}$,$\sum_{i=1}^{5}{x}_{i}^{2}$,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$,代入公式求值,从而得到回归直线方程;
解答 解:(1)根据表中数据:$\overline{x}$=$\frac{1}{5}(2+4+6+8+5)$=5,$\overline{y}$=$\frac{1}{5}(30+40+50+60+70)$=50
方差${S}^{2}=\frac{1}{5}[(30-50)^{2}+(40-50)^{2}+(60-50)^{2}+(50-50)^{2}+(70-50)^{2}]$=200;
(2)由(1)$\overline{x}$=5,$\overline{y}$=50,
又已知$\sum_{i=1}^{5}{x}_{i}^{2}$=145,$\sum_{i=1}^{5}{y}_{1}^{2}$=13500,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=1380;
于是可得:${\;}_{b}^{∧}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)=$\frac{1380-5×5×50}{145-5×{5}^{2}}=6.5$
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=50-6.5×5=17.5;
因此,所求回归直线方程为:$\hat y$=6.5x+17.5.
点评 本题考查了线性回归方程的求法及方差的计算的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
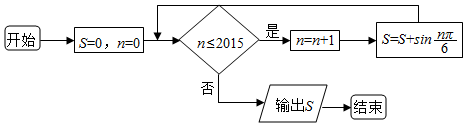
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈[0,1],使x2-1≥0的否定为“?x∈[0,1],都有x2-1<0” | |
| B. | 命题p为假命题,命题q为真命题,则(¬p)∨(¬q)为真命题 | |
| C. | 命题“若x,y均为奇数,则x+y为奇数”及它的逆命题均为假命题 | |
| D. | 命題“若x2+2x=0,则x=0或x=2”的逆否命题为“若x≠0或x≠2,则x2+2x≠0”. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{64}$ | B. | $\frac{1}{64}$ | C. | $\frac{4}{81}$ | D. | $\frac{1}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-4=0 | B. | x-2y+6=0 | C. | x-2y-6=0 | D. | x-2y+4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com