
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$ |
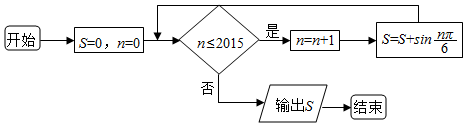
分析 模拟程序框图的运行过程,得出该程序运行后输出的算式S,根据周期性求出s的值即可.
解答 解:s=0,n=0≤2015,n=1,
s=0+sin$\frac{π}{6}$=$\frac{1}{2}$,n=1≤2015,n=2,
s=$\frac{1}{2}$+sin$\frac{π}{3}$=$\frac{1+\sqrt{3}}{2}$,n=2≤2015,n=3,
s=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$+sin$\frac{π}{2}$=$\frac{3+\sqrt{3}}{2}$,n=3≤2015,n=4,
s=$\frac{3+\sqrt{3}}{2}$+sin$\frac{2π}{3}$=$\frac{3+2\sqrt{3}}{2}$,n=4≤2015,n=5,
s=$\frac{3+2\sqrt{3}}{2}$+sin$\frac{5π}{6}$=$\frac{4+2\sqrt{3}}{2}$,n=5≤2015,n=6,
s=$\frac{4+2\sqrt{3}}{2}$+sinπ=$\frac{4+2\sqrt{3}}{2}$,n=6≤2015,n=7,
s=$\frac{4+2\sqrt{3}}{2}$+sin$\frac{7π}{6}$=$\frac{3+2\sqrt{3}}{2}$,n=7≤2015,n=8,
s=$\frac{3+2\sqrt{3}}{2}$+sin$\frac{4π}{3}$=$\frac{3+\sqrt{3}}{2}$,n=8≤2015,n=9,
s=$\frac{3+\sqrt{3}}{2}$+sin$\frac{3π}{2}$=$\frac{1+\sqrt{3}}{2}$,n=9≤2015,n=10,
s=$\frac{1+\sqrt{3}}{2}$+sin$\frac{5π}{3}$=$\frac{1}{2}$,n=10≤2015,n=11,
s=$\frac{1}{2}$+sin$\frac{11π}{6}$=0,
故周期是11,由2015÷9=183×11+2,
故s=$\frac{1}{2}$,n=2014≤2015,n=2015,
s=$\frac{1+\sqrt{3}}{2}$,n=2015≤2015,n=2016,
s=$\frac{3+\sqrt{3}}{2}$,n=2016>2015,
输出s=$\frac{3+\sqrt{3}}{2}$,
故选:D.
点评 本题考查的知识点是程序框图,在写程序的运行结果时,我们常使用模拟循环的办法,但程序的循环体中变量比较多时,要用表格法对数据进行管理,属于基础题.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解葫芦岛市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100),第二组[100,110),…,第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组人数为4.
为了解葫芦岛市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100),第二组[100,110),…,第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组人数为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com