
 如图,在△ABC中,C=$\frac{π}{4}$,角B的平分线BD交AC于点D,设∠CBD=θ,其中θ是直线x-2y+3=0的倾斜角.
如图,在△ABC中,C=$\frac{π}{4}$,角B的平分线BD交AC于点D,设∠CBD=θ,其中θ是直线x-2y+3=0的倾斜角.分析 (1)根据θ是直线x-2y+3=0的倾斜角,求出sinθ和cosθ的值,角B的平分线BD交AC于点D,利用二倍角公式求出cos∠ABC,即可求出sinA;
(2)根据正弦定理求出AC,BC的关系,利用向量的夹角公式求出AC,可得BC,正弦定理可得答案.
解答 解:(1)∵θ是直线x-2y+3=0的倾斜角,∴tanθ=$\frac{1}{2}$,
又θ∈(0,$\frac{π}{2}$),故sinθ=$\frac{1}{\sqrt{5}}$,cosθ=$\frac{2}{\sqrt{5}}$,
则sin∠ABC=sin2θ=2sinθcosθ=2×$\frac{1}{\sqrt{5}}$×$\frac{2}{\sqrt{5}}$=$\frac{4}{5}$,
∴cos∠ABC=2cos2θ-1=2×$\frac{4}{5}$-1=$\frac{3}{5}$,
sinA=sin[π-($\frac{π}{4}$+2θ)]=sin($\frac{π}{4}$+2θ)=$\frac{\sqrt{2}}{2}$(sin2θ+cos2θ)=$\frac{\sqrt{2}}{2}$•($\frac{3}{5}$+$\frac{4}{5}$)=$\frac{7\sqrt{2}}{10}$
(2)由正弦定理,得$\frac{BC}{sinA}$=$\frac{AC}{sin∠ABC}$,即$\frac{BC}{\frac{7\sqrt{2}}{10}}$=$\frac{AC}{\frac{4}{5}}$,
∴BC=$\frac{7\sqrt{2}}{8}$AC.
又$\overrightarrow{CA}$•$\overrightarrow{CB}$=$\frac{\sqrt{2}}{2}$|$\overrightarrow{CB}$|•|$\overrightarrow{CA}$|=28,∴|$\overrightarrow{CB}$|•|$\overrightarrow{CA}$|=28$\sqrt{2}$,
由上两式解得AC=4$\sqrt{2}$,
又由$\frac{AB}{sinC}$=$\frac{AC}{sin∠ABC}$,得$\frac{AB}{\frac{\sqrt{2}}{2}}$=$\frac{AC}{\frac{4}{5}}$,
∴AB=5.
点评 本题考查了二倍角公式和正弦定理的灵活运用和计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈[0,1],使x2-1≥0的否定为“?x∈[0,1],都有x2-1<0” | |
| B. | 命题p为假命题,命题q为真命题,则(¬p)∨(¬q)为真命题 | |
| C. | 命题“若x,y均为奇数,则x+y为奇数”及它的逆命题均为假命题 | |
| D. | 命題“若x2+2x=0,则x=0或x=2”的逆否命题为“若x≠0或x≠2,则x2+2x≠0”. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
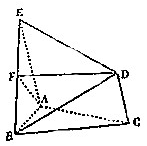 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 16 |
| 成绩不优秀 | 38 | 46 | 84 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com