
| A. | (-∞,4-8ln2] | B. | (-∞,$\frac{17}{4}$-8ln2] | C. | (-∞,4+8ln2] | D. | (-∞,$\frac{17}{4}$+8ln2] |
分析 运用参数分离,可得a≤(x+$\frac{1}{x}$+$\frac{lnx}{x}$)min,对任意的x∈[$\frac{1}{4}$,+∞)恒成立,令g(x)=x+$\frac{1}{x}$+$\frac{lnx}{x}$,x$≥\frac{1}{4}$,求出导数,再求导数,通过最小值判断g(x)的导数大于0,进而得到g(x)的最小值,即可得到a的范围.
解答 解:不等式$\frac{f(x)}{x}$+lnx+1≥0对任意的x∈[$\frac{1}{4}$,+∞)恒成立,即为
x(x-a)+lnx+1≥0对任意的x∈[$\frac{1}{4}$,+∞)恒成立,
即a≤(x+$\frac{1}{x}$+$\frac{lnx}{x}$)min,
令g(x)=x+$\frac{1}{x}$+$\frac{lnx}{x}$,x$≥\frac{1}{4}$,
则g′(x)=1-$\frac{1}{{x}^{2}}$+$\frac{1-lnx}{{x}^{2}}$=$\frac{{x}^{2}-lnx}{{x}^{2}}$,
令h(x)=x2-lnx,x$≥\frac{1}{4}$,
h′(x)=2x-$\frac{1}{x}$,当$\frac{1}{4}$$≤x<\frac{\sqrt{2}}{2}$时,h′(x)<0,h(x)递减;
当x>$\frac{\sqrt{2}}{2}$时,h′(x)>0,h(x)递增.
即有x=$\frac{\sqrt{2}}{2}$处h(x)取得最小值,且为$\frac{1}{2}$-ln$\frac{\sqrt{2}}{2}$>0,
则h(x)>0在x$≥\frac{1}{4}$恒成立,即有g′(x)>0,
则g(x)在[$\frac{1}{4}$,+∞)递增,
即有x=$\frac{1}{4}$处g(x)取得最小值且为$\frac{17}{4}$-8ln2.
则a≤$\frac{17}{4}$-8ln2.
故选:B.
点评 本题考查导数的运用:求单调区间和最值,同时考查不等式恒成立问题转化为求函数的最值问题,运用参数分离和构造函数,运用单调性求最值是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{7}^{1}$×$\frac{1}{3}$×($\frac{2}{3}$) | B. | C${\;}_{7}^{2}$×($\frac{1}{3}$)2×($\frac{2}{3}$)5 | C. | C${\;}_{7}^{3}$×($\frac{1}{3}$)3×($\frac{2}{3}$) | D. | C${\;}_{7}^{4}$×($\frac{1}{3}$)4×($\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos(x-$\frac{3π}{2}$) | B. | y=sin2x-cos2x | C. | y=cos2$\frac{x}{2}$ | D. | y=tan2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
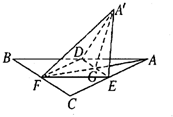 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 异面直线A′E与BD不可能垂直 | |
| B. | 恒有平面A′GF⊥平面BCDE | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 动点A′在平面ABC上的射影在线段AF上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com