
分析 (1)由4Tn=12Sn+13n,可得当n≥2时,4Tn-1=12Sn-1+13(n-1),4bn=12an+13,代入即可得出;
(2)由(1)得:cn=-3n,于是 $\frac{100}{{c}_{n}{c}_{n+1}}$=$\frac{100}{9}(\frac{1}{n}-\frac{1}{n+1})$.利用“裂项求和”与不等式的性质即可得出.
解答 解:(1)∵4Tn=12Sn+13n,
∴当n≥2时,4Tn-1=12Sn-1+13(n-1),4bn=12an+13,
∴${b}_{n}=3{a}_{n}+\frac{13}{4}$=-3n-$\frac{5}{4}$.又b1=-$\frac{17}{4}$也适合上式,
∴数列{bn}的通项公式为bn=-3n-$\frac{5}{4}$.
(2)由(1)得:cn=bn+$\frac{5}{4}$=-3n,
于是 $\frac{100}{{c}_{n}{c}_{n+1}}$=$\frac{100}{9}(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{100}{{c}_{1}•{c}_{2}}$+$\frac{100}{{c}_{2}•{c}_{3}}$+…+$\frac{100}{{c}_{n}•{c}_{n+1}}$=$\frac{100}{9}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+$…+$(\frac{1}{n}-\frac{1}{n+1})]$=$\frac{100}{9}(1-\frac{1}{n+1})$=$\frac{100}{9}$$•\frac{n}{n+1}$,
令$\frac{100}{9}$$•\frac{n}{n+1}$>11,解得n>99,
∴n的最小值为100.
点评 本题考查了递推式的应用、“裂项求和”与不等式的性质,考查了推理能力与计算能力,属于中档题.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,4-8ln2] | B. | (-∞,$\frac{17}{4}$-8ln2] | C. | (-∞,4+8ln2] | D. | (-∞,$\frac{17}{4}$+8ln2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
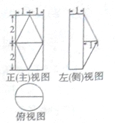
| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a(1+p)5 | B. | a(1+p)6 | C. | $\frac{a}{p}$[(1+p)5-(1+p)] | D. | $\frac{a}{p}$[(1+p)6-(1+p)] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| y | 5 | 6 | 12 | 14 | 20 | 23 | 25 |
| A. | 47 | B. | 52 | C. | 55 | D. | 38 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com