练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．在数列-1，0，$\frac{1}{9}$，$\frac{1}{8}$，…，$\frac{n-2}{{n}^{2}}$，…中，0.08是它的（　　）
    A．第100项B．第12项C．第10项D．第8项

    分析 令$\frac{n-2}{{n}^{2}}$=0.08，解出即可得出．

    解答 解：令$\frac{n-2}{{n}^{2}}$=0.08，化为：2n2-25n+50=0，
    解得n=10，或n=$\frac{5}{2}$（舍去）．
    故选：C．

    点评 本题考查了数列的通项公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知向量$\overrightarrow{a}$=（1，1），$\overrightarrow b=（-3，\;1）$，若k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$垂直，则实数k=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设$\frac{dy}{dx}$=$\frac{x}{y}$，y|x=0=4，则微分方程的通解为$\frac{1}{2}{y}^{2}-\frac{1}{2}{x}^{2}+C=0$；特解为$\frac{1}{2}{y}^{2}-\frac{1}{2}{x}^{2}-8=0$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设z为复数，D为满足条件||z|-1|+|z|-1=0的点Z所构成的图形的边界．
    （1）若复数W=$\frac{1}{2}$z+1-2i（其中z∈D），试证明：表示复数W的点在某一圆上运动，并写出此圆的复数方程；
    （2）若满足条件|z+$\frac{1}{2}$|=|z-$\frac{3}{2}$i|的点所构成的图形D′与D有两个公共点A，B，且OA，OB的倾斜角分别为α，β（O为原点），求cos（α+β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若函数f（x）=2x+2-x的定义域为R，则（　　）
    A．f（x）为偶函数B．f（x）为奇函数
    C．f（x）既奇又偶函数D．f（x）为非奇非偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．下列命题中是全称命题且为真命题的序号为①③．
    ①圆有内接正方形，②$\sqrt{3}＞\sqrt{2}$，③指数函数都是单调函数，④常数列都是等比数列，⑤两个正数的算术平均数大于它们的几何平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知（1+x）+（1+x）2+（1+x）3+…+（1+x）10=a0+a1x+a2x2+…+a10x10（x≠-1，x≠0）．求a3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，在同一平面内，∠AOB=150°，∠AOC=120°，|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=3，|$\overrightarrow{OC}$|=4．
    （1）试用$\overrightarrow{OB}$和$\overrightarrow{OC}$表示$\overrightarrow{OA}$；
    （2）是否存在实数λ，使得$\overrightarrow{AD}$=$λ\overrightarrow{AC}$，$\overrightarrow{AC}$$•\overrightarrow{BD}$=0同时成立？若存在，求出λ的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

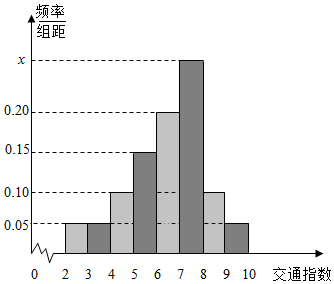    2．交通指数是指交通拥堵指数或交通运行指数（Traffic Performance Index，即“TPI”），是反应道路畅通或拥堵的概念性数值，交通指数的取值范围为0～10，分为五级：0～2畅通，2～4为基本畅通，4～6轻度畅通，6～8为中度拥堵，8～10为严重拥堵．高峰时段，巴中市交通指挥中心随机选取了市区40个交通路段，依据交通指数数据绘制的频率分布直方图如图所示：
    （Ⅰ）  求出图中x的值，并计算这40个路段中为“中度拥堵”的有多少个？
    （Ⅱ） 在我市区的40个交通路段中用分层抽样的方法抽取容量为20的样本．从这个样本路段的“基本畅通”和“严重拥堵”路段中随机选出2个路段，求其中只有一个是“严重拥堵”路段的概率．

    查看答案和解析>>

    同步练习册答案