
| 3 |
| a |
| 3 |
| a |
| a |
| 2 |
| 3 |
| a |
| a2 |
| 4 |
| 3 |
| a |
| 3 |
| a |
| a |
| 2 |
| 3 |
| a |
| a2 |
| 4 |
| a |
| 2 |
| 3 |
| a |
| a |
| 2 |
| 3 |
| a |
| 3 |
| 2 |
| a |
| 2 |
|
| 3 |
| a |


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
A、对于线性回归方程
| ||||||||||
| B、茎叶图的优点在于它可以保存原始数据,并且可以随时记录 | ||||||||||
| C、将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变 | ||||||||||
| D、掷一枚均匀硬币连续出现5次正面,第6次掷这枚硬币一定出现反面 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
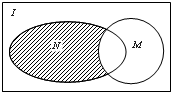 设全集I是实数集R.M={x|x>2或x<-2}与N={x|1<x<3}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R.M={x|x>2或x<-2}与N={x|1<x<3}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A、{x|x<2} |
| B、{x|-2≤x<1} |
| C、{x|1<x≤2} |
| D、{x|-2≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com