
已知曲线 y = x3 + x-2 在点 P0 处的切线  平行直线
平行直线
4x-y-1=0,且点 P0 在第三象限,
求P0的坐标; ⑵若直线  , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
(1)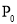 的坐标为
的坐标为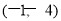 ⑵
⑵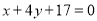
【解析】
试题分析:(1)根据曲线方程求出导函数,因为已知直线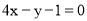 的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点
的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点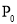 的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;
的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;
(2)由直线l1的斜率为4,根据两直线垂直时斜率的乘积为-1,得到直线l的斜率为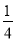 - ,又根据(1)中求得的切点坐标,写出直线l的方程即可.
- ,又根据(1)中求得的切点坐标,写出直线l的方程即可.
⑴由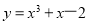 ,得
,得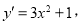
由已知得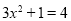 ,解之得
,解之得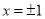 .当
.当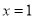 时,
时,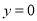 ;当
;当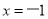 时,
时,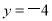 .
.
又∵点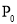 在第三象限,
在第三象限,
∴切点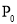 的坐标为
的坐标为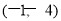 .
.
⑵∵直线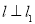 ,
,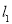 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为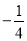 ,
,
∵l过切点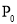 ,点
,点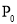 的坐标为
的坐标为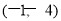 )
)
∴直线l的方程为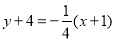 即
即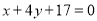 .
.
考点:利用导数研究曲线上某点切线方程.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某几何体是由直三棱柱与圆锥的组合体,其直观图和三视图如图所示,正视图为正方形,其中俯视图中椭圆的离心率为

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设 、
、 分别是椭圆
分别是椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆
在椭圆 上,线段
上,线段 的中点在
的中点在 轴上,若
轴上,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com