
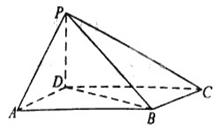
如图,四棱锥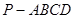 中,底面
中,底面 为平行四边形,
为平行四边形,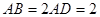 ,
,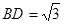 ,
,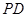 ⊥底面
⊥底面 .
.
(1)证明:平面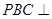 平面
平面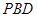 ;
;
(2)若二面角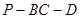 为
为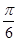 ,求
,求 与平面
与平面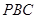 所成角的正弦值.
所成角的正弦值.
(1)证明过程详见解析;(2)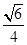 .
.
解析试题分析:(1)可以遵循思路面面垂直 线面垂直
线面垂直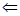 线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明
线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明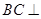 面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即
面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即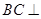 BD,
BD, 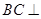 PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
(2)求线面夹角可以利用三维空间直角坐标系,分别以DA,DB,PD三条两两垂直的直线建立坐标系,求面法向量与直线的夹角的余弦值的绝对值即为线面夹角的余弦值.
试题解析:
(1)∵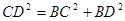 ∴
∴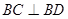
又∵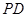 ⊥底面
⊥底面 ∴
∴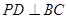
又∵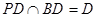 ∴
∴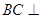 平面
平面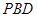
而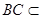 平面
平面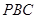 ∴平面
∴平面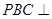 平面
平面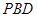 5分
5分
(1)由(1)所证,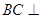 平面
平面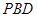 ,所以∠
,所以∠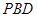 即为二面角P-BC-D的平面角,即∠
即为二面角P-BC-D的平面角,即∠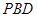
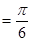
而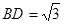 ,所以
,所以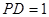 7分
7分
分别以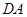 、
、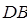 、
、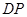 为
为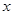 轴、
轴、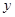 轴、
轴、 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则 ,
, ,
,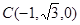 ,
, 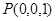 ,所以,
,所以,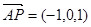 ,
,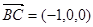 ,
,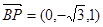 ,设平面
,设平面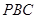 的法向量为
的法向量为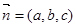 ,则
,则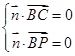 ,即
,即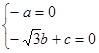 可解得
可解得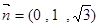 ∴
∴ 与平面
与平面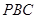 所成角的正弦值为
所成角的正弦值为 12分
12分
考点:面面垂直 线面夹角


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
如图,四棱柱 中,
中,
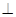 底面
底面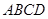 .四边形
.四边形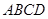 为梯形,
为梯形, ,且
,且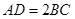 .过
.过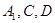 三点的平面记为
三点的平面记为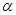 ,
,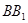 与
与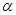 的交点为
的交点为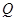 .
.
(1)证明: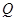 为
为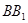 的中点;
的中点;
(2)求此四棱柱被平面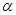 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;
(3)若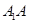
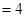 ,
,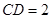 ,梯形
,梯形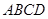 的面积为6,求平面
的面积为6,求平面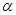 与底面
与底面 所成二面角大小.
所成二面角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直角梯形ABCP中,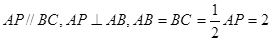 ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为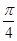 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.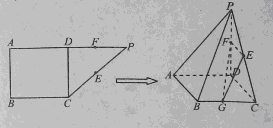
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知在四棱锥 中,底面
中,底面 是矩形,
是矩形,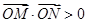 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的点.
上的点.
(1)当 是
是 的中点时,求证:
的中点时,求证: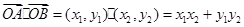 平面
平面 ;
;
(2)要使二面角 的大小为
的大小为 ,试确定
,试确定 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且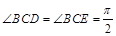 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证:AG 平面BDE;
平面BDE;
(2)求:二面角G DE
DE B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB∥A1B1,AB=2A1B1=2DD1=2a.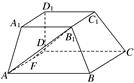
(1)求异面直线AB1与DD1所成角的余弦值;
(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com