
分析 构造函数f(x)=x5+2015x,可得f(x)为奇函数,且是定义在R上的增函数,结合已知可得f(a+1)=-f(b+1),即(a+1)=-(b+1),进而得到答案.
解答 解:令f(x)=x5+2015x,
则f(-x)=-f(x)恒成立,即f(x)为奇函数,
又由f′(x)=5x4+2015>0恒成立,
∴f(x)是定义在R上的增函数,
∵$\left\{\begin{array}{l}{(a+1)^{5}+2015(a+1)=-1}\\{(b+1)^{5}+2015(b+1)=1}\end{array}\right.$,
即f(a+1)=-f(b+1),
∴(a+1)=-(b+1),即a+b=-2,
故答案为:-2
点评 本题考查的知识点是函数奇偶性,函数的单调性,构造出函数将问题转化为函数的性质应用,是解答的关键.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
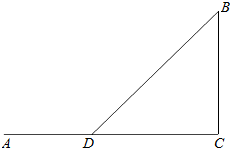 如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.
如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com