
分析 根据直线和圆相交的弦长公式,求出m,n的关系,结合基本不等式进行求解即可.
解答 解:圆心C(m,n),半径R=3,
∵圆心在第一象限,
∴m>0,n>0.
∵直线l:x+2y+2=0与圆C相交的弦长为4,
∴圆心到直线的距离d=$\sqrt{{R}^{2}-{2}^{2}}=\sqrt{9-4}$=$\sqrt{5}$,
即$\frac{|m+2n+2|}{\sqrt{5}}=\sqrt{5}$,即m+2n+2=5,
则m+2n=3,即$\frac{m}{3}$+$\frac{2n}{3}$=1,
则$\frac{m+2n}{mn}$=($\frac{1}{n}$+$\frac{2}{m}$)×($\frac{m}{3}$+$\frac{2n}{3}$)=$\frac{2}{3}$+$\frac{2}{3}$+$\frac{m}{3n}$+$\frac{4n}{3m}$≥$\frac{4}{3}$+2$•\sqrt{\frac{m}{3n}•\frac{4n}{3m}}$=$\frac{4}{3}+\frac{4}{3}$=$\frac{8}{3}$,
当且仅当$\frac{m}{3n}$=$\frac{4n}{3m}$,即m=2n时取等号,
故答案为:$\frac{8}{3}$.
点评 本题主要考查基本不等式的应用,根据直线与圆相交的性质,利用1的代换是解决本题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,1] | C. | [1,2] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
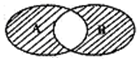 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )| A. | {x|0<x<2} | B. | {x|1<x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x≤1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com