
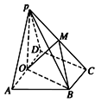
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.分析 (1)根据AD∥BC,BC=$\frac{1}{2}$AD,O为AD的中点可得四边形BCDO为平行四边形,则CD∥BO,从而OB⊥AD,平面PAD⊥平面ABCD且平面PAD∩平面ABCD=AD,根据面面垂直的性质可知,BO⊥平面PAD,
(2)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系.利用向量法能求出t的值.
解答 证明:(1)∵AD∥BC,BC=$\frac{1}{2}$AD,O为AD的中点.
∴四边形BCDO为平行四边形,∴CD∥BO.
∵∠ADC=90°,∴∠AOB=90°,即OB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BO⊥平面PAD.
解:(2)∵PA=PD,O为AD的中点.∴PO⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD(6分)
如图,以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系.
则平面BOC的一个法向量为$\overrightarrow{n}$=(0,0,1),
O(0,0,0),P(0,0,$\sqrt{3}$),B(0,$\sqrt{3}$,0),C(-1,$\sqrt{3}$,0).
设M(x,y,z),PM=tMC
$由\overrightarrow{PM}=(x,y,z-\sqrt{3})$,$\overrightarrow{MC}=(-1-x,\sqrt{3}-y,-z)$
则x=-$\frac{t}{1+t}$,y=$\frac{\sqrt{3}t}{1+t}$,z=$\frac{\sqrt{3}}{1+t}$,
∴$\overrightarrow{OM}=(-\frac{t}{1+t},\frac{\sqrt{3}t}{1+t},\frac{\sqrt{3}}{1+t})$,$\overrightarrow{OB}=(0,\sqrt{3},0)$,
设平面MBO的法向量为$\overrightarrow{m}$=(a,b,c),
$由\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{OB}=\sqrt{3}b=0}\\{\overrightarrow{m}•\overrightarrow{OM}=-\frac{t}{1+t}a+\frac{\sqrt{3}t}{1+t}b+\frac{\sqrt{3}}{1+t}c=0\\;\\;}\end{array}\right.$可取$\overrightarrow{m}$=($\sqrt{3}$,0,t)
∵二面角M-BO-C的大小为45°
∴cos45°=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=$\frac{t}{\sqrt{3+{t}^{2}}}=\frac{1}{\sqrt{2}}$,解得t=$\sqrt{3}$
∴在线段PC上是存在点M,PM=$\sqrt{3}$MC,使得二面角M-BO-C的大小为45°.
点评 本题考查线面垂直的证明,向量法确定动点位置,是中档题,解题时要认真审题,注意向量法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ | C. | $\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AD}$ | D. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [0,2$\sqrt{2}$] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
设 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称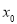 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如下:


(1)求李老师这8天“健步走”步数的平均数;
(2)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com