
 如图,已知棱长为4的正方体ABCD-A'B'C'D',M是正方形BB'C'C的中心,P是△A'C'D内(包括边界)的动点,满足PM=PD,则点P的轨迹长度为$\sqrt{14}$.
如图,已知棱长为4的正方体ABCD-A'B'C'D',M是正方形BB'C'C的中心,P是△A'C'D内(包括边界)的动点,满足PM=PD,则点P的轨迹长度为$\sqrt{14}$. 分析 满足PM=PD的点P的轨迹是过MD的中点,且与MD垂直的平面,根据P是△A′C′D内(包括边界)的动点,可得点P的轨迹是两平面的交线ST.T在中点,S在4等分点,利用余弦定理,求出ST即可.
解答 解:满足PM=PD的点P的轨迹是过MD的中点,且与MD垂直的平面,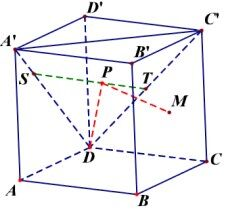
∵P是△A′C′D内(包括边界)的动点,
∴点P的轨迹是两平面的交线ST.T在中点,
S在4等分点时,SD=3$\sqrt{2}$,SM=$\sqrt{{4}^{2}+2}$=3$\sqrt{2}$,满足SD=SM.
∴SD=3$\sqrt{2}$,TD=2$\sqrt{2}$
∴ST2=$(3\sqrt{2})^{2}+(2\sqrt{2})^{2}$-2×$3\sqrt{2}×2\sqrt{2}$×cos60°=14.
∴ST=$\sqrt{14}$.
故答案为:$\sqrt{14}$.
点评 本题考查了空间位置关系、垂直平分线的性质、线面垂直的判定与性质定理、余弦定理,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (${\frac{2}{3}$,1) | B. | (0,1) | C. | (0,$\frac{2}{3}}$) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -21 | B. | -32 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
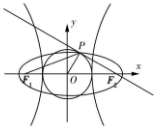 如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为2,以双曲线C的实轴为直径的圆记为圆O,过点F2作圆O的切线,切点为P,则以F1,F2为焦点,过点P的椭圆T的离心率为( )
如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为2,以双曲线C的实轴为直径的圆记为圆O,过点F2作圆O的切线,切点为P,则以F1,F2为焦点,过点P的椭圆T的离心率为( )| A. | $\frac{{\sqrt{5}-\sqrt{3}}}{2}$ | B. | $\sqrt{5}-\sqrt{3}$ | C. | $\frac{{\sqrt{7}-\sqrt{3}}}{4}$ | D. | $\sqrt{7}-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[e-\frac{1}{e},e)$ | B. | [1,e+1) | C. | [e,e+1) | D. | $(e-\frac{1}{e},e+1)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com